«Το τρίπτυχο της γεωμετρίας» (70 λεπτά)
Το Πυθαγόρειο Θεώρημα αποτελεί ένα από τα διασημότερα θεωρήματα στον κόσμο των μαθηματικών. Σύμφωνα με το θεώρημα του Πυθαγόρα, στην Ευκλείδια Γεωμετρία, συσχετίζονται τα τετράγωνα των πλευρών ενός ορθογωνίου τριγώνου ως εξής: “το τετράγωνο της υποτείνουσας ενός ορθογώνιου τριγώνου ισούται με το άθροισμα των τετραγώνων των δύο καθέτων πλευρών”. Το Πυθαγόρειο Θεώρημα ισχύει και αντίστροφα, δηλαδή, αν ισχύει η παρακάτω σχέση μεταξύ των πλευρών ενός τριγώνου, τότε το τρίγωνο είναι ορθογώνιο. Αν και το θεώρημα σήμερα φέρει το όνομα του Έλληνα μαθηματικού Πυθαγόρα (570 π.Χ.- 495 π.Χ.), από ιστορικές έρευνες πιθανολογείται να είχε διατυπωθεί και νωρίτερα ως εμπειρική παρατήρηση. Για το Πυθαγόρειο θεώρημα έχουν δοθεί οι πιο πολλές διαφορετικές αποδείξεις που έχουν δοθεί για μαθηματικό θεώρημα. Ο καθηγητής Elisha Scott Loomis (1852 – 1940) στο βιβλίο του “The Pythagorean Proposition1” συγκέντρωσε 367 διαφορετικές αποδείξεις, οι οποίες περιλαμβάνουν ιστορικό, επιστημονικό καθώς και διδακτικό ενδιαφέρον.
Η ταινία Möbius (Μόμπιους) είναι ένα συναρπαστικό αντικείμενο στον τομέα της τοπολογίας και των μαθηματικών, γνωστό για τις μοναδικές του ιδιότητες. Είναι μία μη προσανατολίσιμη επιφάνεια, κάτι που σημαίνει ότι έχει μόνο μία πλευρά και μία ακμή. Μπορεί εύκολα να κατασκευαστεί παίρνοντας μια λωρίδα χαρτιού, δίνοντάς της μία μισή στροφή και ενώνοντας τα άκρα της για να σχηματιστεί ένας δακτύλιος. Το αποτέλεσμα είναι η ταινία Möbius. Η ταινία Möbius πήρε το όνομά της από τον Γερμανό μαθηματικό και αστρονόμο August Ferdinand Möbius που την ανακάλυψε ανεξάρτητα από τον επίσης Γερμανό μαθηματικό Johann Benedict Listing το 1858. Είναι ένα από τα πρώτα αντικείμενα που μελετήθηκαν στην τοπολογία, τον κλάδο των μαθηματικών που ασχολείται με τις ιδιότητες των χώρων που διατηρούνται υπό συνεχείς παραμορφώσεις.
Οι ευθειογενείς καμπύλες είναι ένα ιδιαίτερο είδος καμπύλων γραμμών που χρησιμοποιούνται συχνά σε διάφορα μαθηματικά και φυσικά προβλήματα. Η βασική τους ιδιότητα είναι ότι κάθε τόξο της καμπύλης μεταξύ δύο σημείων μπορεί να είναι η συντομότερη απόσταση μεταξύ αυτών των σημείων σε μια δεδομένη επιφάνεια ή χώρο.
Τα Στοιχεία του Ευκλείδη αποτελούν ένα από τα πιο εμβληματικά και επιδραστικά έργα στην ιστορία των μαθηματικών, αλλά και των επιστημών γενικότερα. Γραμμένο περίπου το 300 π.Χ. στην Αλεξάνδρεια, το έργο αυτό αποτελεί μια συστηματική και μεθοδική συλλογή γεωμετρικών γνώσεων, οργανωμένων με τρόπο που τα καθιστά προσιτά και λογικά συνεκτικά. Ο Ευκλείδης, χρησιμοποιώντας μια αυστηρά λογική προσέγγιση, κατάφερε να οργανώσει τις προϋπάρχουσες γνώσεις της γεωμετρίας σε ένα ενιαίο, συνεκτικό σύστημα, το οποίο αποτέλεσε τη βάση για τη μαθηματική σκέψη και εκπαίδευση για περισσότερα από δύο χιλιάδες χρόνια.
Δομή των Στοιχείων
Τα Στοιχεία αποτελούνται από δεκατρία βιβλία, καθένα από τα οποία ασχολείται με διαφορετικές πλευρές της γεωμετρίας και άλλων μαθηματικών πεδίων. Ο Ευκλείδης ξεκινά με τις βασικές έννοιες και θεμελιώδη αξιώματα και συνεχίζει να αναπτύσσει πιο σύνθετες θεωρίες και προτάσεις. Η αυστηρή δομή του έργου είναι ένα από τα βασικά του χαρακτηριστικά. Τα θεωρήματα αποδεικνύονται με έναν λογικό και συστηματικό τρόπο, χρησιμοποιώντας τα αρχικά αξιώματα και προτάσεις που έχουν ήδη αποδειχθεί. Αξιώματα και Ορισμοί
Το έργο ξεκινά με μια σειρά από ορισμούς, αξιώματα και κοινές έννοιες, που αποτελούν τα θεμέλια για την ανάπτυξη των θεωρημάτων. Οι ορισμοί παρέχουν τις θεμελιώδεις έννοιες της γεωμετρίας, όπως το σημείο, η γραμμή, και το επίπεδο, ενώ τα αξιώματα (ή ποστουλάτα) είναι προτάσεις που θεωρούνται αυτονόητες και δεν απαιτούν απόδειξη. Για παράδειγμα, ένα από τα πιο γνωστά αξιώματα είναι το πέμπτο αξίωμα, γνωστό ως “παράλληλο αξίωμα,” το οποίο αναφέρει ότι δύο ευθείες σε ένα επίπεδο που δεν τέμνονται είναι παράλληλες.
Θεωρήματα και Αποδείξεις
Με βάση τα αξιώματα, ο Ευκλείδης προχωρά στην απόδειξη θεωρημάτων, τα οποία είναι προτάσεις που αποδεικνύονται ως αληθείς μέσω λογικής και μαθηματικής συλλογιστικής. Η μέθοδος αυτή είναι γνωστή ως “αξιωματική μέθοδος” και αποτέλεσε θεμελιώδη πρακτική για τα μαθηματικά και τις φυσικές επιστήμες. Ο Ευκλείδης ήταν πρωτοπόρος στη χρήση αυτής της μεθόδου για την ανάπτυξη γεωμετρικών θεωρημάτων, και το έργο του έχει χρησιμεύσει ως πρότυπο για πολλές μεταγενέστερες επιστημονικές εργασίες.
Κάθε βιβλίο των Στοιχείων ασχολείται με διαφορετικές πτυχές της γεωμετρίας. Για παράδειγμα, τα πρώτα έξι βιβλία ασχολούνται με την επίπεδη γεωμετρία, ενώ τα επόμενα βιβλία επεκτείνονται στη θεωρία των αριθμών, την αναλογία, και τη στερεομετρία. Τα θεωρήματα που παρουσιάζονται σε κάθε βιβλίο είναι οργανωμένα με τέτοιο τρόπο ώστε η απόδειξη του ενός να βασίζεται στην απόδειξη του προηγούμενου, δημιουργώντας έτσι μια λογική αλληλουχία που οδηγεί στη γενική κατανόηση των γεωμετρικών αρχών.
Η Επίδραση των Στοιχείων
Τα Στοιχεία του Ευκλείδη είχαν τεράστια επιρροή στη μαθηματική εκπαίδευση και έρευνα για πάνω από δύο χιλιάδες χρόνια. Κατά τη διάρκεια του Μεσαίωνα και της Αναγέννησης, το έργο μεταφράστηκε σε πολλές γλώσσες και χρησιμοποιήθηκε ως το κύριο εγχειρίδιο διδασκαλίας για τη γεωμετρία. Η αυστηρότητα της λογικής και η σαφήνεια των αποδείξεων έκαναν τα Στοιχεία ένα από τα πιο σεβαστά και μελετημένα κείμενα στην ιστορία των μαθηματικών.
Η επιρροή των Στοιχείων δεν περιορίστηκε μόνο στα μαθηματικά. Η μεθοδολογία του Ευκλείδη, με την έμφαση στη λογική και τη συστηματική απόδειξη, επηρέασε βαθιά άλλους τομείς της γνώσης, όπως η φιλοσοφία και η επιστημολογία. Οι ιδέες του για τη λογική και τη δομή της γνώσης ενσωματώθηκαν στη σκέψη φιλοσόφων και επιστημόνων, επηρεάζοντας την ανάπτυξη της δυτικής φιλοσοφίας και της επιστήμης.
Η Διαχρονική Σημασία των Στοιχείων
Παρά την πρόοδο των μαθηματικών και την ανάπτυξη νέων κλάδων, τα Στοιχεία του Ευκλείδη παραμένουν επίκαιρα και διαχρονικά. Η μεθοδολογία της αυστηρής απόδειξης που εισήγαγε ο Ευκλείδης αποτελεί ακόμα το θεμέλιο για τη μαθηματική σκέψη και εκπαίδευση. Σήμερα, οι μαθητές συνεχίζουν να μελετούν τα θεωρήματα του Ευκλείδη ως μέρος της εκπαίδευσής τους στη γεωμετρία, και η επιρροή του έργου του παραμένει ζωντανή.
Η διαχρονική αξία των Στοιχείων έγκειται στην ικανότητά τους να παρέχουν ένα συνεκτικό και λογικά οργανωμένο σύστημα γνώσης, το οποίο μπορεί να χρησιμοποιηθεί ως βάση για την κατανόηση όχι μόνο της γεωμετρίας, αλλά και των αρχών της λογικής και της επιστημονικής μεθοδολογίας. Το έργο του Ευκλείδη είναι ένα κλασικό παράδειγμα του πώς η ανθρώπινη σκέψη μπορεί να συστηματοποιήσει τη γνώση και να δημιουργήσει μια διαχρονική κληρονομιά που εξακολουθεί να επηρεάζει την εκπαίδευση και την επιστήμη μέχρι σήμερα.
Ιστορικό Πλαίσιο και Ζωή του Πυθαγόρα:
Ο Πυθαγόρας γεννήθηκε στη Σάμο, ένα νησί του Αιγαίου, γύρω στο 572 π.Χ. Σύμφωνα με τις ιστορικές πηγές, ταξίδεψε ευρέως κατά τη διάρκεια της ζωής του, επισκεπτόμενος την Αίγυπτο και τη Βαβυλώνα, όπου ήρθε σε επαφή με τις φιλοσοφικές και μαθηματικές παραδόσεις αυτών των πολιτισμών. Αυτές οι εμπειρίες συνέβαλαν στη διαμόρφωση των ιδεών του και στην ανάπτυξη της διδασκαλίας του. Μετά την επιστροφή του στη Σάμο, ο Πυθαγόρας ίδρυσε τη δική του σχολή, η οποία σύντομα μεταφέρθηκε στον Κρότωνα της Μεγάλης Ελλάδας (σημερινή Νότια Ιταλία). Η Πυθαγόρεια Σχολή δεν ήταν απλώς ένα μαθηματικό ινστιτούτο, αλλά μια κοινότητα που συνδύαζε φιλοσοφία, επιστήμη, θρησκεία και πολιτική σκέψη. Τα μέλη της σχολής ακολουθούσαν έναν αυστηρό τρόπο ζωής, με βασικές αρχές την πειθαρχία, την απλότητα και την κοινοκτημοσύνη.
Οι Πυθαγόρειες Διδασκαλίες και το Σύστημα Αριθμών:
Οι Πυθαγόρειοι πίστευαν ότι οι αριθμοί ήταν η ουσία της πραγματικότητας. Η αριθμητική και η γεωμετρία δεν ήταν απλώς εργαλεία για την επίλυση προβλημάτων, αλλά αντιπροσώπευαν τη θεμελιώδη δομή του σύμπαντος. Οι μαθηματικές σχέσεις και οι αναλογίες θεωρούνταν εκδηλώσεις της αρμονίας και της τάξης που διέπουν τη φύση Ένα από τα βασικά στοιχεία των Πυθαγόρειων διδασκαλιών ήταν η έννοια των “τελείων αριθμών” και των “φίλων αριθμών”. Τέλειος αριθμός είναι ένας αριθμός που ισούται με το άθροισμα των διαιρετών του (εκτός του εαυτού του), όπως ο αριθμός 28 (1 + 2 + 4 + 7 + 14 = 28). Οι φίλοι αριθμοί είναι δύο αριθμοί όπου το άθροισμα των διαιρετών του ενός ισούται με τον άλλον, όπως το ζεύγος 220 και 284.
Το Πυθαγόρειο Θεώρημα και η Γεωμετρία:
Το Πυθαγόρειο Θεώρημα είναι ίσως η πιο γνωστή μαθηματική πρόταση που συνδέεται με τον Πυθαγόρα. Αυτό το θεώρημα δεν αναπτύχθηκε αποκλειστικά από τον ίδιο τον Πυθαγόρα, καθώς είναι γνωστό ότι πολιτισμοί όπως οι Βαβυλώνιοι γνώριζαν την ιδιότητα αυτή πριν από την εποχή του Πυθαγόρα. Ωστόσο, η προσέγγισή του και η μαθηματική του απόδειξη αποτέλεσαν σημαντική πρόοδο στη συστηματική μελέτη της γεωμετρίας. Το Πυθαγόρειο Θεώρημα λέει ότι σε ένα ορθογώνιο τρίγωνο, το άθροισμα των τετραγώνων των δύο καθέτων πλευρών (οι πλευρές που σχηματίζουν τη γωνία των 90 μοιρών) ισούται με το τετράγωνο της υποτείνουσας (η πλευρά απέναντι από τη γωνία των 90 μοιρών). Αυτό το θεώρημα είναι βασικό για πολλές εφαρμογές στην αρχιτεκτονική, την τριγωνομετρία, την πλοήγηση και άλλους τομείς.
Μουσική Θεωρία και Αρμονία:
Ο Πυθαγόρας δεν περιορίστηκε μόνο στα μαθηματικά. Η συμβολή του στη μουσική θεωρία είναι εξίσου σημαντική. Ανακάλυψε τις μαθηματικές αναλογίες που αντιστοιχούν στις μουσικές αρμονίες, διαπιστώνοντας ότι τα διαστήματα μεταξύ των μουσικών τόνων μπορούν να εκφραστούν με απλούς λόγους μικρών ακέραιων αριθμών. Αυτή η ιδέα επηρέασε τη μουσική θεωρία για αιώνες και η σύνδεση μεταξύ μαθηματικών και μουσικής είναι μια από τις πιο γνωστές πτυχές της Πυθαγόρειας σκέψης.
Πυθαγόρειος Τρόπος Ζωής:
Η Πυθαγόρεια Σχολή δεν ήταν απλώς μια ακαδημαϊκή κοινότητα, αλλά και μια θρησκευτική και φιλοσοφική αδελφότητα με αυστηρούς κανόνες ζωής. Τα μέλη της ζούσαν σε κοινότητα, ακολουθούσαν μια αυστηρή διατροφή (που περιλάμβανε τη χορτοφαγία), και αφιέρωναν τον χρόνο τους στη μελέτη, τον διαλογισμό και τη μουσική. Οι Πυθαγόρειοι πίστευαν στην αθανασία της ψυχής και στην μετενσάρκωση. Αυτή η πίστη επηρέασε βαθιά τον τρόπο ζωής τους και την αντίληψή τους για τη ζωή και το σύμπαν. Οι διδασκαλίες τους είχαν επίσης μυστικιστικό χαρακτήρα, και η γνώση μεταδιδόταν μόνο στους μυημένους.
Επιρροή και Κληρονομιά:
Η Πυθαγόρεια σκέψη συνέχισε να ασκεί μεγάλη επιρροή και μετά τον θάνατο του Πυθαγόρα. Οι ιδέες του επηρέασαν τη φιλοσοφία του Πλάτωνα και τον Νεοπλατωνισμό, καθώς και άλλες φιλοσοφικές και επιστημονικές παραδόσεις. Στην Αναγέννηση, οι Πυθαγόρειες ιδέες αναβίωσαν και επηρέασαν τη σκέψη των λογίων της εποχής, ιδιαίτερα στον τομέα της αστρονομίας και της μουσικής. Η κληρονομιά του Πυθαγόρα παραμένει ζωντανή μέχρι σήμερα. Οι ιδέες του για τη μαθηματική αρμονία του σύμπαντος εξακολουθούν να είναι αντικείμενο μελέτης και διδασκαλίας, και το Πυθαγόρειο Θεώρημα παραμένει μια θεμελιώδης αρχή στη γεωμετρία. Η σύνδεση μεταξύ αριθμών, μουσικής και κοσμικής τάξης που προωθούσε ο Πυθαγόρας συνεχίζει να εμπνέει επιστήμονες, φιλοσόφους και καλλιτέχνες σε όλο τον κόσμο.
Ο Θαλής ο Μιλήσιος, ένας από τους επτά σοφούς της αρχαίας Ελλάδας, υπήρξε από τους πρώτους που θεμελίωσαν την ελληνική μαθηματική σκέψη. Γεννήθηκε στη Μίλητο γύρω στο 624 π.Χ. και είναι γνωστός για την προσφορά του στα μαθηματικά, τη γεωμετρία και την αστρονομία. Το έργο του άνοιξε τον δρόμο για την ανάπτυξη της γεωμετρίας και της φιλοσοφίας των φυσικών επιστημών.
Συμβολή του Θαλή στα Μαθηματικά:
Ο Θαλής θεωρείται ο πατέρας της ελληνικής γεωμετρίας. Μία από τις πιο γνωστές συνεισφορές του είναι το θεώρημα του Θαλής, που αφορά την αναλογία των πλευρών δύο τριγώνων που είναι παρόμοια. Σύμφωνα με το θεώρημα, αν μια ευθεία τέμνει δύο πλευρές ενός τριγώνου και είναι παράλληλη προς την τρίτη πλευρά, τότε τα δύο τρίγωνα που σχηματίζονται είναι παρόμοια, και οι αντίστοιχες πλευρές τους είναι ανάλογες. Αυτό είναι ένα από τα θεμέλια της αναλογικής σκέψης στα μαθηματικά και χρησιμοποιείται ευρέως στη γεωμετρία και την τριγωνομετρία.
Η Μέτρηση των Πυραμίδων:
Μία από τις πιο γνωστές ιστορίες σχετικά με τον Θαλής είναι η μέτρηση του ύψους της Μεγάλης Πυραμίδας της Γκίζας. Σύμφωνα με την παράδοση, ο Θαλής χρησιμοποίησε τις σκιές για να υπολογίσει το ύψος της πυραμίδας. Υπολόγισε την αναλογία της σκιάς του σώματός του με το ύψος του και τη σύγκρινε με την αναλογία της σκιάς της πυραμίδας με το ύψος της. Αυτή η μέθοδος βασίζεται στις αρχές της γεωμετρίας και των αναλογιών που ανέπτυξε ο ίδιος.
Αστρονομία και Φιλοσοφία:
Εκτός από τη γεωμετρία, ο Θαλής ασχολήθηκε και με την αστρονομία. Προέβλεψε την έκλειψη του ηλίου το 585 π.Χ., ένα γεγονός που θεωρήθηκε σημαντική επιτυχία εκείνη την εποχή και ενίσχυσε τη φήμη του ως σοφού. Ο Θαλής ήταν επίσης από τους πρώτους που διατύπωσε την ιδέα ότι η Γη είναι ένας δίσκος που επιπλέει στο νερό, μια θεωρία που, αν και σήμερα φαίνεται απλοϊκή, αποτέλεσε μια από τις πρώτες προσπάθειες κατανόησης της φύσης του κόσμου μέσω της παρατήρησης και της λογικής.
Παραλληλία και Αναλογίες:
Η έννοια της παραλληλίας και των αναλογιών είναι κεντρική στα μαθηματικά και αναπτύχθηκε σε μεγάλο βαθμό από τον Θαλής. Η παραλληλία, δηλαδή η ιδιότητα δύο ευθειών να μην τέμνονται, αποτελεί βασικό συστατικό της ευκλείδειας γεωμετρίας. Οι αναλογίες, από την άλλη πλευρά, είναι θεμελιώδεις για την κατανόηση της σχέσης μεταξύ διαφορετικών μεγεθών και χρησιμοποιούνται ευρέως στην επίλυση γεωμετρικών προβλημάτων.
Κληρονομιά:
Ο Θαλής έθεσε τις βάσεις για τη μαθηματική και φιλοσοφική σκέψη που ακολούθησε στην αρχαία Ελλάδα. Το έργο του επηρέασε σημαντικά τους επόμενους μαθηματικούς, όπως ο Πυθαγόρας και ο Ευκλείδης, και η προσέγγισή του για την κατανόηση του κόσμου μέσω της λογικής και της παρατήρησης παραμένει θεμελιώδης στη σύγχρονη επιστήμη.
Η κληρονομιά του Θαλής, μέσα από τα θεωρήματα, τις αρχές της γεωμετρίας και τις φιλοσοφικές του ιδέες, συνεχίζει να διδάσκεται και να αναγνωρίζεται ως βασικό κομμάτι της ιστορίας των μαθηματικών και της επιστήμης.
«Ένα Σύμπαν φτιαγμένο από αριθμούς» (50 λεπτά)
- Οι Πραγματικοί Αριθμοί και οι Άρρητοι Αριθμοί:
Οι πραγματικοί αριθμοί (συμβολίζονται ως R) αποτελούν μια ευρεία κατηγορία αριθμών που περιλαμβάνει τόσο τους ρητούς όσο και τους άρρητους αριθμούς. Οι ρητοί αριθμοί είναι εκείνοι που μπορούν να γραφούν ως κλάσμα δύο ακέραιων αριθμών, δηλαδή της μορφής 𝑝𝑞𝑝𝑞𝑞𝑝 , όπου ppp και qqq είναι ακέραιοι και 𝑞≠0𝑞≠0𝑞=0 . Ωστόσο, όχι όλοι οι αριθμοί μπορούν να γραφούν ως τέτοια κλάσματα. Οι αριθμοί που δεν μπορούν να εκφραστούν ως κλάσμα δύο ακέραιων είναι οι άρρητοι αριθμοί. Οι άρρητοι αριθμοί είναι εξαιρετικά σημαντικοί διότι γεφυρώνουν τα κενά ανάμεσα στους ρητούς αριθμούς, επιτρέποντας ένα πλήρες και συνεκτικό αριθμητικό σύστημα που περιγράφει συνεχείς ποσότητες.
- Χρυσή Τομή (φ):
Η Χρυσή Τομή, με τιμή περίπου 1,6180339887…, είναι ένας από τους πιο διάσημους άρρητους αριθμούς. Εμφανίζεται σε πολλούς τομείς, από την τέχνη και την αρχιτεκτονική μέχρι τη φύση και τη βιολογία. Έχει μια ιδιαίτερη γεωμετρική ιδιότητα: αν διαιρέσουμε ένα τμήμα σε δύο μέρη έτσι ώστε η αναλογία του συνολικού μήκους προς το μεγαλύτερο τμήμα να είναι η ίδια με την αναλογία του μεγαλύτερου τμήματος προς το μικρότερο, τότε το αποτέλεσμα είναι η Χρυσή Τομή.
Η Χρυσή Τομή συνδέεται στενά με τα μοτίβα ανάπτυξης στη φύση, όπως οι σπείρες που εμφανίζονται στα κοχύλια και τα φυτά. Επιπλέον, χρησιμοποιείται στην τέχνη για να δημιουργήσει αισθητικά ευχάριστες αναλογίες.
- Ο Αριθμός π:
Ο αριθμός π, με τιμή περίπου 3,1415926535…, είναι ένας από τους πιο διάσημους άρρητους αριθμούς και έχει χρησιμοποιηθεί εδώ και αιώνες στη γεωμετρία, ειδικά στην μελέτη των κύκλων. Η αναλογία της περιφέρειας ενός κύκλου προς τη διάμετρό του είναι πάντοτε ίση με π, ανεξαρτήτως του μεγέθους του κύκλου.
Αυτός ο αριθμός είναι επίσης θεμελιώδης στην τριγωνομετρία και την ανάλυση, καθώς εμφανίζεται σε πολλές μαθηματικές εκφράσεις, όπως στην ανάλυση Fourier και στην επίλυση διαφορικών εξισώσεων.
- Ο Αριθμός του Νεπέρ (e):
Ο αριθμός e, με τιμή περίπου 2,7182818284…, είναι εξίσου σημαντικός στην ανάλυση, ιδίως στη μελέτη των εκθετικών λειτουργιών και των φυσικών λογαρίθμων. Αυτός ο αριθμός είναι η βάση των φυσικών λογαρίθμων και έχει εφαρμογές σε πολλούς τομείς των μαθηματικών, από την θεωρία των πιθανοτήτων μέχρι την οικονομία και τη φυσική.
Η λειτουργία ex περιγράφει την εκθετική αύξηση, που εμφανίζεται σε πολλές φυσικές και οικονομικές διαδικασίες, όπως η αύξηση των πληθυσμών, η ραδιενεργή αποσύνθεση και η απόδοση της σύνθετης επένδυσης.
- Σχέση Ρητών και Άρρητων Αριθμών:
Μια από τις πιο συναρπαστικές ιδιότητες των πραγματικών αριθμών είναι ότι ανάμεσα σε οποιοδήποτε δύο ρητούς αριθμούς υπάρχει ένας άπειρος αριθμός άρρητων αριθμών. Αυτό σημαίνει ότι οι άρρητοι αριθμοί είναι πυκνοί στο σύνολο των πραγματικών αριθμών, καθιστώντας το ένα συνεχές σύνολο χωρίς κενά. Η κατανόηση αυτής της ιδιότητας είναι θεμελιώδης για την ανάλυση, καθώς επιτρέπει τη μελέτη συνεχών φαινομένων όπως οι συναρτήσεις, οι γραμμές και τα επίπεδα.
- Γεωμετρικές Αναπαραστάσεις και οι Φυσικές Δομές:
Οι αριθμοί όπως η Χρυσή Τομή και το π συχνά συνδέονται με γεωμετρικές δομές και μοτίβα στη φύση. Η Χρυσή Τομή εμφανίζεται στις σπείρες που παρατηρούμε στα κελύφη των μαλακίων και στην κατανομή των φύλλων γύρω από ένα στέλεχος. Η σπείρα αυτή ακολουθεί τη σειρά Fibonacci, μια άλλη μαθηματική ακολουθία που σχετίζεται με τη Χρυσή Τομή.
Επιπλέον, ο αριθμός π εμφανίζεται σε κάθε μορφή που έχει κυκλική συμμετρία ή σφαιρική γεωμετρία, ενώ ο αριθμός e εμφανίζεται σε φυσικές διαδικασίες που περιγράφονται από εκθετική ανάπτυξη ή αποσύνθεση.
- Οι Πραγματικοί Αριθμοί στα Μαθηματικά και τη Φυσική:
Οι πραγματικοί αριθμοί είναι θεμελιώδεις στη μαθηματική ανάλυση, η οποία μελετά τις ιδιότητες των συναρτήσεων, των σειρών, και των ακολουθιών. Η μελέτη των ορίων, της συνέχειας, των παραγώγων και των ολοκληρωμάτων βασίζεται στους πραγματικούς αριθμούς, καθιστώντας τους κρίσιμους για τη σύγχρονη επιστήμη και τεχνολογία.
Στη φυσική, οι πραγματικοί αριθμοί χρησιμοποιούνται για να περιγράψουν συνεχείς ποσότητες, όπως μήκη, χρόνους, θερμοκρασίες και δυναμικά, προσφέροντας μια πλήρη και ακριβή κατανόηση των φυσικών φαινομένων.
Συμπέρασμα:
Οι πραγματικοί και άρρητοι αριθμοί αποτελούν θεμελιώδεις έννοιες στη μαθηματική θεωρία και τη φυσική επιστήμη. Από την αρχαία Ελλάδα μέχρι τη σύγχρονη εποχή, η κατανόηση αυτών των αριθμών και των ιδιοτήτων τους έχει επιτρέψει την ανάπτυξη της γεωμετρίας, της ανάλυσης, και της φυσικής, ενώ συνεχίζει να είναι ένα ζωτικό μέρος της επιστημονικής και τεχνολογικής προόδου. Οι μαθηματικές τους ιδιότητες και οι εφαρμογές τους στη φύση υποδεικνύουν τη βαθιά σύνδεση των αριθμών με τις βασικές δομές του σύμπαντος.
«Στα όρια του Απείρου» (60 λεπτά)
Ο Αρχιμήδης ήταν ένας από τους πιο επιδραστικούς μαθηματικούς της αρχαιότητας και η συνεισφορά του στον υπολογισμό εμβαδών και όγκων έθεσε τα θεμέλια για τον μετέπειτα απειροστικό λογισμό. Ο τρόπος με τον οποίο αντιμετώπισε αυτά τα προβλήματα ήταν πρωτοποριακός για την εποχή του και επηρέασε βαθιά την ανάπτυξη των μαθηματικών.
Υπολογισμός Εμβαδών και Όγκων:
Ο Αρχιμήδης χρησιμοποίησε τη μέθοδο της εξάντλησης για να υπολογίσει το εμβαδόν και τον όγκο διάφορων σχημάτων και στερεών. Αυτή η μέθοδος είναι ένας πρόδρομος της σύγχρονης ολοκληρωτικής μεθόδου και βασίζεται στην ιδέα του υπολογισμού ενός μεγέθους μέσω της προσέγγισής του με τη χρήση όλο και μικρότερων τμημάτων.
Μέθοδος της Εξάντλησης:
Η μέθοδος της εξάντλησης του Αρχιμήδη περιλάμβανε τη διαίρεση ενός σχήματος σε όλο και μικρότερα τμήματα, για να προσεγγιστεί το εμβαδόν ή ο όγκος του σχήματος αυτού. Ένα παράδειγμα αυτής της μεθόδου είναι ο υπολογισμός του εμβαδού του κύκλου μέσω της εγγραφής πολυγώνων με όλο και περισσότερες πλευρές μέσα στον κύκλο. Καθώς ο αριθμός των πλευρών αυξάνεται, το εγγεγραμμένο πολύγωνο προσεγγίζει όλο και περισσότερο τον κύκλο, επιτρέποντας μια ολοένα και πιο ακριβή προσέγγιση του εμβαδού του.
Η Σημασία της Άθροισης:
Ο Αρχιμήδης κατάλαβε ότι το κλειδί για τον υπολογισμό αυτών των μεγεθών ήταν η άθροιση πολλών μικρών τμημάτων. Για παράδειγμα, για να υπολογίσει τον όγκο μιας σφαίρας, την προσέγγισε χρησιμοποιώντας λεπτές φέτες (κυλινδρικούς δίσκους), το άθροισμα των οποίων δίνει τον όγκο της σφαίρας.
Αυτή η διαδικασία άθροισης είναι ουσιαστικά το θεμέλιο του ολοκληρωτικού λογισμού, που αναπτύχθηκε πλήρως χιλιάδες χρόνια αργότερα από μαθηματικούς όπως ο Νεύτωνας και ο Λάιμπνιτς. Ο ολοκληρωτικός λογισμός επιτρέπει τον υπολογισμό του συνολικού εμβαδού ή όγκου ενός σχήματος μέσω της αθροιστικής προσέγγισης απείρως μικρών τμημάτων.
Η Κληρονομιά του Αρχιμήδη:
Η επιρροή του Αρχιμήδη στους υπολογισμούς και την κατανόηση των γεωμετρικών σχημάτων παραμένει εμφανής μέχρι σήμερα. Η χρήση της μεθόδου της εξάντλησης και η αντίληψη ότι τα γεωμετρικά σχήματα μπορούν να προσεγγιστούν μέσω απειροστικών διαδικασιών ήταν θεμελιώδη βήματα προς την ανάπτυξη της μαθηματικής ανάλυσης.
Ο Αρχιμήδης έδειξε επίσης ότι οι άπειρες διαδικασίες και τα απειροελάχιστα δεν είναι απλώς φιλοσοφικές έννοιες, αλλά μπορούν να χρησιμοποιηθούν για την ακριβή επίλυση πρακτικών μαθηματικών προβλημάτων. Οι τεχνικές του ήταν τόσο προηγμένες που χρησιμοποιήθηκαν για πάνω από δύο χιλιάδες χρόνια, έως ότου αναπτύχθηκαν περαιτέρω από τους μαθηματικούς της Αναγέννησης και της Εποχής των Φώτων.
Συμπέρασμα:
Ο Αρχιμήδης άνοιξε τον δρόμο για την ανάπτυξη του απειροστικού λογισμού μέσω της μεθόδου της εξάντλησης και της άθροισης απείρως μικρών τμημάτων. Οι μεθοδολογίες του παραμένουν θεμελιώδεις στη μαθηματική εκπαίδευση και την κατανόηση της γεωμετρίας και της ανάλυσης, και η κληρονομιά του συνεχίζει να επηρεάζει τη σύγχρονη επιστήμη και τεχνολογία.
Ο Απειροστικός Λογισμός είναι ένας από τους πιο σημαντικούς τομείς των μαθηματικών, με βασική εφαρμογή στον υπολογισμό ορίων, παραγώγων και ολοκληρωμάτων. Ένα από τα κεντρικά θέματα του απειροστικού λογισμού είναι η εύρεση του μήκους μιας καμπύλης και η προσέγγιση με όρια, γνωστή ως οριακή προσέγγιση. Αυτές οι μέθοδοι αποτέλεσαν τη βάση για την ανάπτυξη της μαθηματικής ανάλυσης και έχουν σημαντικές εφαρμογές σε πολλές επιστημονικές και τεχνολογικές περιοχές.
Η Αρχή της Οριακής Προσέγγισης:
Η οριακή προσέγγιση είναι η διαδικασία κατά την οποία προσεγγίζουμε ένα πρόβλημα με τη χρήση ολοένα και μικρότερων τμημάτων. Αυτή η ιδέα είναι θεμελιώδης για την κατανόηση του μήκους μιας καμπύλης, τον υπολογισμό του εμβαδού μιας επιφάνειας ή ακόμα και την εκτίμηση όγκων. Η ιδέα είναι ότι, καθώς τα τμήματα που χρησιμοποιούμε γίνονται απείρως μικρά, το συνολικό άθροισμα των τμημάτων αυτών προσεγγίζει την ακριβή τιμή του μεγέθους που υπολογίζουμε.
Υπολογισμός του Μήκους μιας Καμπύλης:
Μία από τις κύριες εφαρμογές της οριακής προσέγγισης στον απειροστικό λογισμό είναι ο υπολογισμός του μήκους μιας καμπύλης. Για να υπολογίσουμε το μήκος μιας καμπύλης, μπορούμε να προσεγγίσουμε την καμπύλη με μία σειρά από ευθύγραμμα τμήματα. Καθώς αυτά τα τμήματα γίνονται όλο και μικρότερα, η συνολική απόσταση που προσεγγίζει τη συνολική καμπύλη γίνεται όλο και πιο ακριβής.
Η Συμβολή του Αρχιμήδη:
Ο Αρχιμήδης, ένας από τους μεγαλύτερους μαθηματικούς της αρχαιότητας, έκανε τεράστιες προόδους στη χρήση της οριακής προσέγγισης για τον υπολογισμό εμβαδών και όγκων. Ένα από τα πιο γνωστά του έργα είναι η εύρεση της προσέγγισης του αριθμού π μέσω της χρήσης πολυγώνων εγγεγραμμένων και περιγεγραμμένων σε έναν κύκλο. Με τη χρήση όλο και μεγαλύτερων πολυγώνων, ο Αρχιμήδης κατάφερε να προσεγγίσει τον αριθμό π με πολύ μεγάλη ακρίβεια.
Ο Αρχιμήδης εφάρμοσε επίσης την ιδέα του απειροστικού λογισμού στη μελέτη των καμπυλών και των εμβαδών, βάζοντας τα θεμέλια για τη μεταγενέστερη ανάπτυξη της μαθηματικής ανάλυσης.
Απειροστικός Λογισμός και Μοντέρνα Μαθηματικά:
Η ανάπτυξη του απειροστικού λογισμού από τον Αρχιμήδη και άλλους αρχαίους μαθηματικούς αποτελεί το θεμέλιο για τη σύγχρονη μαθηματική ανάλυση. Οι μέθοδοι αυτοί χρησιμοποιούνται ευρέως σε πολλούς τομείς, όπως η μηχανική, η φυσική και η τεχνολογία, προσφέροντας ακριβείς και αποτελεσματικές λύσεις για τη μοντελοποίηση και την ανάλυση πολύπλοκων συστημάτων.
Συμπερασματικά, ο απειροστικός λογισμός και η χρήση οριακών προσεγγίσεων αποτελούν κεντρικές έννοιες στα μαθηματικά, επιτρέποντας την ακριβή περιγραφή και ανάλυση των συνεχών φαινομένων που απαντώνται στη φύση και στην επιστήμη. Η κληρονομιά των αρχαίων μαθηματικών, όπως ο Αρχιμήδης, συνεχίζει να επηρεάζει τη σύγχρονη σκέψη και έρευνα, διατηρώντας τη σημασία της στις μαθηματικές και επιστημονικές κοινότητες.
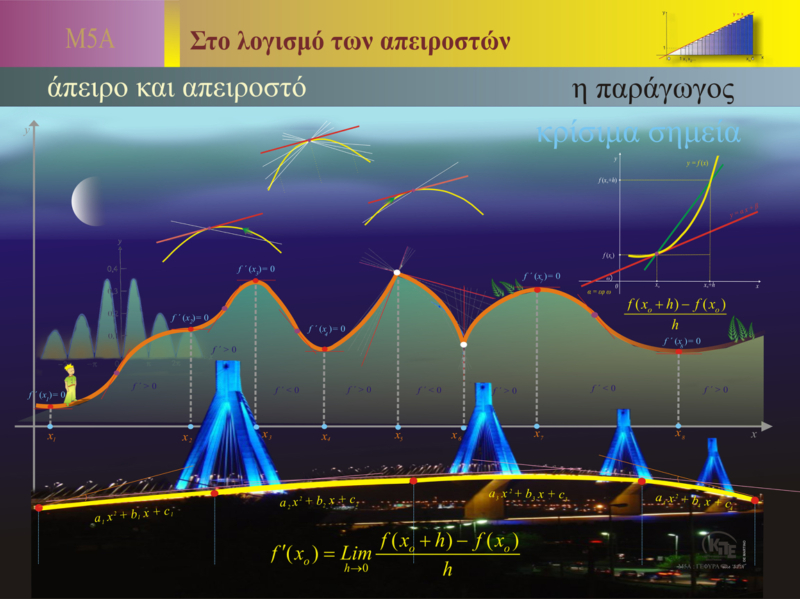
Ο απειροστικός λογισμός είναι ένας θεμελιώδης τομέας των μαθηματικών που ασχολείται με την έννοια του απείρου και του απειροστού. Η παράγωγος είναι μια από τις κεντρικές έννοιες του απειροστικού λογισμού, και έχει κρίσιμη σημασία για την κατανόηση της συμπεριφοράς των συναρτήσεων, καθώς και για την επίλυση προβλημάτων που αφορούν τις μεταβολές.
Παράγωγος μιας Συνάρτησης:
Η παράγωγος μιας συνάρτησης σε ένα σημείο περιγράφει τον ρυθμό μεταβολής της συνάρτησης σε σχέση με την ανεξάρτητη μεταβλητή της. Η παράγωγος δίνεται από το όριο της μέσης κλίσης της συνάρτησης καθώς η μεταβολή της μεταβλητής πλησιάζει στο μηδέν.
Κρίσιμα Σημεία και Μέγιστα/Ελάχιστα:
Τα κρίσιμα σημεία μιας συνάρτησης είναι τα σημεία όπου η παράγωγος της συνάρτησης είναι μηδέν ή δεν ορίζεται. Σε αυτά τα σημεία, η συνάρτηση μπορεί να έχει τοπικά μέγιστα, ελάχιστα ή σημεία καμπής. Για παράδειγμα, αν η παράγωγος αλλάζει πρόσημο από θετικό σε αρνητικό, το σημείο είναι πιθανό να είναι τοπικό μέγιστο, ενώ αν αλλάζει από αρνητικό σε θετικό, το σημείο είναι πιθανό να είναι τοπικό ελάχιστο.
Η μελέτη των κρίσιμων σημείων είναι σημαντική για την εύρεση των μέγιστων και ελάχιστων τιμών μιας συνάρτησης, κάτι που είναι κρίσιμο σε πολλά πρακτικά προβλήματα, όπως η βελτιστοποίηση και η ανάλυση κόστους.
Απειροστό και Απείρως Μεγάλο:
Στον απειροστικό λογισμό, οι έννοιες του απειροστού και του απείρως μεγάλου είναι θεμελιώδεις. Το απειροστό είναι μια ποσότητα τόσο μικρή που είναι σχεδόν μηδενική, αλλά όχι ακριβώς μηδέν. Αυτές οι ποσότητες χρησιμοποιούνται για να περιγράψουν μικροσκοπικές μεταβολές σε φυσικά μεγέθη, όπως η ταχύτητα ενός αντικειμένου σε ένα συγκεκριμένο σημείο της τροχιάς του.
Το απείρως μεγάλο, από την άλλη πλευρά, είναι μια ποσότητα τόσο μεγάλη που δεν έχει πεπερασμένο όριο. Οι μαθηματικοί χρησιμοποιούν αυτά τα δύο άκρα για να περιγράψουν και να κατανοήσουν τη συμπεριφορά των συναρτήσεων και των συστημάτων που παρουσιάζουν ακραίες τιμές.
Εφαρμογές της Παραγώγου:
Η παράγωγος έχει ευρύτατες εφαρμογές στη φυσική, τη μηχανική, την οικονομία και άλλους τομείς. Για παράδειγμα, στην κινηματική, η παράγωγος της θέσης ως προς τον χρόνο δίνει την ταχύτητα, ενώ η παράγωγος της ταχύτητας δίνει την επιτάχυνση. Στην οικονομία, η παράγωγος μπορεί να χρησιμοποιηθεί για να βρεθεί ο ρυθμός αλλαγής της ζήτησης σε σχέση με την τιμή ενός προϊόντος.
Συμπέρασμα:
Η παράγωγος είναι ένα από τα πιο ισχυρά εργαλεία του απειροστικού λογισμού και επιτρέπει την ανάλυση των αλλαγών και των μεταβολών σε ένα ευρύ φάσμα εφαρμογών. Η κατανόηση των παραγώγων και των κρίσιμων σημείων μιας συνάρτησης είναι κρίσιμη για την επίλυση προβλημάτων βελτιστοποίησης και την κατανόηση της συμπεριφοράς των φυσικών συστημάτων. Η χρήση του απείρου και του απειροστού στον λογισμό παρέχει τα απαραίτητα μαθηματικά εργαλεία για την αντιμετώπιση σύνθετων και δυναμικών προβλημάτων στον πραγματικό κόσμο.
Ο απειροστικός λογισμός είναι ένα από τα πιο ισχυρά και θεμελιώδη εργαλεία στα μαθηματικά, με δύο κύριους πυλώνες: τη διαφορική και την ολοκληρωτική ανάλυση. Η ολοκλήρωση είναι η διαδικασία εύρεσης του εμβαδού κάτω από μια καμπύλη, και αποτελεί μια από τις κεντρικές έννοιες της ολοκληρωτικής ανάλυσης.
Η Έννοια της Ολοκλήρωσης:
Η ολοκλήρωση σχετίζεται στενά με την έννοια του ορίου και της άθροισης.
Ολοκλήρωμα Riemann:
Ο Georg Friedrich Bernhard Riemann, ένας από τους πιο σημαντικούς μαθηματικούς του 19ου αιώνα, ανέπτυξε την έννοια του ολοκληρώματος Riemann, το οποίο αποτελεί το θεμέλιο της κλασικής θεωρίας ολοκλήρωσης.
Από την Άθροιση στην Ολοκλήρωση:
Η μετάβαση από την άθροιση στην ολοκλήρωση είναι μια κεντρική ιδέα στα μαθηματικά. Ενώ η άθροιση είναι πεπερασμένη και αφορά συγκεκριμένο αριθμό όρων, η ολοκλήρωση αναφέρεται στη διαδικασία λήψης του ορίου μιας άπειρης ακολουθίας αθροισμάτων καθώς τα τμήματα γίνονται απείρως μικρά. Αυτή η διαδικασία είναι κρίσιμη για τον ακριβή υπολογισμό εμβαδών, όγκων και άλλων φυσικών ποσοτήτων.
Θεμελιώδες Θεώρημα του Απειροστικού Λογισμού:
Το θεμελιώδες θεώρημα του απειροστικού λογισμού συνδέει τη διαφορική ανάλυση με την ολοκληρωτική ανάλυση.
Εφαρμογές της Ολοκλήρωσης:
Η ολοκλήρωση έχει ευρύτατες εφαρμογές σε πολλούς τομείς. Στη φυσική, χρησιμοποιείται για τον υπολογισμό εμβαδών, όγκων, έργου και ενέργειας. Στη μηχανική, είναι κρίσιμη για την ανάλυση κατασκευών και τη μελέτη δυναμικών συστημάτων. Στην οικονομία, οι ολοκληρώσεις χρησιμοποιούνται για τη μοντελοποίηση συσσωρευτικών ποσοτήτων όπως το συνολικό κόστος ή το συνολικό κέρδος.
Συμπέρασμα:
Η ολοκλήρωση είναι ένας θεμελιώδης μηχανισμός για την κατανόηση και την ανάλυση συνεχών ποσοτήτων. Μέσα από την έννοια του ολοκληρώματος, οι μαθηματικοί και οι επιστήμονες μπορούν να υπολογίζουν εμβαδά, όγκους και άλλες σημαντικές ποσότητες με ακρίβεια. Η ανάπτυξη της θεωρίας του ολοκληρώματος από μαθηματικούς όπως ο Riemann ήταν κρίσιμη για την εξέλιξη των μαθηματικών και των επιστημών γενικότερα, προσφέροντας τα απαραίτητα εργαλεία για την ανάλυση και την κατανόηση του φυσικού κόσμου.
«Πάρτο αλλιώς» (50 λεπτά)
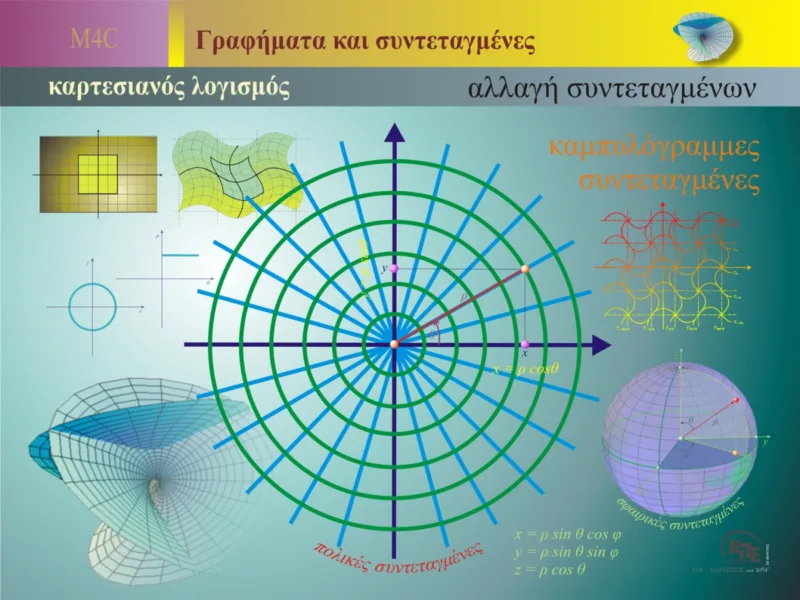
Οι καμπυλόγραμμες συντεταγμένες είναι ένα εξαιρετικά σημαντικό εργαλείο στη γεωμετρία και τη φυσική, επιτρέποντας την αναπαράσταση και την ανάλυση προβλημάτων που δεν μπορούν να αντιμετωπιστούν εύκολα με το παραδοσιακό καρτεσιανό σύστημα συντεταγμένων. Οι καμπυλόγραμμες συντεταγμένες είναι ιδιαίτερα χρήσιμες όταν μελετάμε συστήματα που έχουν κυκλική, σφαιρική ή άλλη μη ευθύγραμμη συμμετρία.
Πολικές Συντεταγμένες:
Οι πολικές συντεταγμένες είναι ένα σύστημα καμπυλόγραμμων συντεταγμένων που χρησιμοποιείται κυρίως για την αναπαράσταση σημείων σε ένα επίπεδο. Σε αυτό το σύστημα, ένα σημείο αναπαρίσταται με δύο τιμές: την απόσταση από ένα σταθερό σημείο (συνήθως το κέντρο ή την αρχή των αξόνων) και τη γωνία θ σε σχέση με έναν σταθερό άξονα (συνήθως τον οριζόντιο άξονα).
Αυτό το σύστημα είναι ιδιαίτερα χρήσιμο για την περιγραφή κυκλικών και σπειροειδών σχημάτων, καθώς και για την ανάλυση φαινομένων που περιλαμβάνουν γωνιακή συμμετρία.
Σφαιρικές και Κυλινδρικές Συντεταγμένες:
Οι σφαιρικές συντεταγμένες επεκτείνουν την ιδέα των πολικών συντεταγμένων σε τρεις διαστάσεις. Σε αυτό το σύστημα, ένα σημείο στο χώρο καθορίζεται από την απόσταση από το κέντρο, τη γωνία θ σε σχέση με τον κατακόρυφο άξονα και μια δεύτερη γωνία ϕ που αντιπροσωπεύει την περιστροφή γύρω από τον κατακόρυφο άξονα.
Οι κυλινδρικές συντεταγμένες είναι μια άλλη επέκταση των πολικών συντεταγμένων σε τρεις διαστάσεις, κατάλληλη για συστήματα με συμμετρία γύρω από έναν άξονα. Σε αυτό το σύστημα, ένα σημείο καθορίζεται από την απόσταση r από τον άξονα, τη γωνία θ και το ύψος z κατά μήκος του άξονα.
Χρήσεις των Καμπυλόγραμμων Συντεταγμένων:
Οι καμπυλόγραμμες συντεταγμένες χρησιμοποιούνται ευρέως στη φυσική, τη μηχανική και τη γεωμετρία για την ανάλυση συστημάτων που δεν είναι βολικά να περιγραφούν με ευθύγραμμες συντεταγμένες. Για παράδειγμα, οι σφαιρικές συντεταγμένες είναι ιδανικές για τη μελέτη φαινομένων που έχουν σφαιρική συμμετρία, όπως η κατανομή ηλεκτρικών φορτίων γύρω από ένα σημειακό φορτίο ή οι κινήσεις ενός πλανήτη γύρω από τον ήλιο.
Οι καμπυλόγραμμες συντεταγμένες είναι επίσης χρήσιμες στη μελέτη των επιφανειών και των γεωμετρικών σχημάτων που δεν είναι ευθύγραμμα. Μπορούν να χρησιμοποιηθούν για την περιγραφή επιφανειών σε τρισδιάστατο χώρο, όπως η επιφάνεια ενός κύκλου ή μιας σφαίρας.
Μετατροπή Συντεταγμένων:
Ένα σημαντικό εργαλείο στη χρήση των καμπυλόγραμμων συντεταγμένων είναι η ικανότητα να μετατρέπουμε από το ένα σύστημα συντεταγμένων στο άλλο. Οι σχέσεις μετατροπής επιτρέπουν τη μετάβαση από καρτεσιανές συντεταγμένες σε πολικές, σφαιρικές ή κυλινδρικές συντεταγμένες και το αντίστροφο.
Συμπέρασμα:
Οι καμπυλόγραμμες συντεταγμένες προσφέρουν ευελιξία και αποτελεσματικότητα στην ανάλυση γεωμετρικών και φυσικών προβλημάτων που δεν μπορούν να περιγραφούν εύκολα με καρτεσιανό σύστημα. Με τη χρήση αυτών των συντεταγμένων, οι επιστήμονες και οι μηχανικοί μπορούν να μελετήσουν πιο περίπλοκα συστήματα και να κατανοήσουν βαθύτερα τις ιδιότητες και τις σχέσεις των φυσικών φαινομένων.
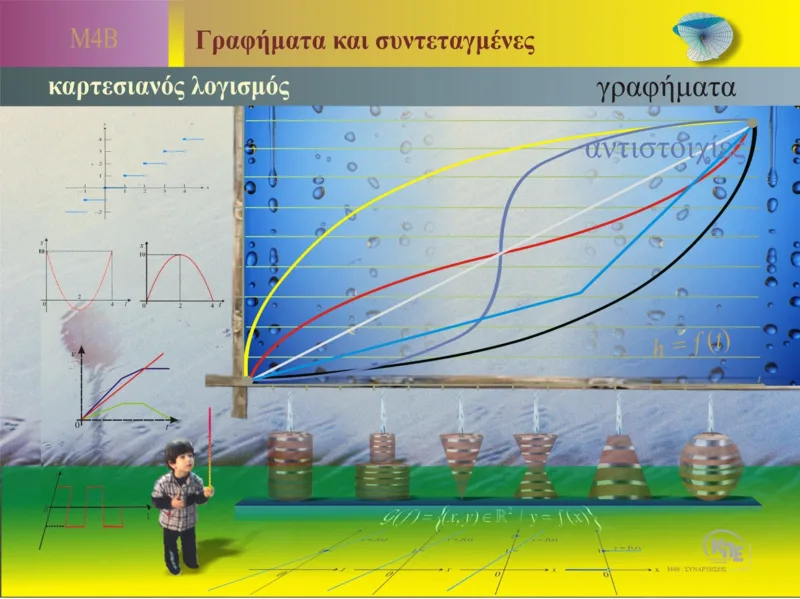
Ο καρτεσιανός λογισμός και τα γραφήματα είναι ουσιαστικά εργαλεία για την κατανόηση και την αναπαράσταση των μαθηματικών συναρτήσεων και των σχέσεων μεταξύ των μεταβλητών. Οι έννοιες αυτές είναι κεντρικές στη μαθηματική ανάλυση, τη φυσική, την οικονομία και πολλές άλλες επιστήμες.
Καρτεσιανός Λογισμός:
Ο καρτεσιανός λογισμός βασίζεται στο καρτεσιανό σύστημα συντεταγμένων, το οποίο επιτρέπει την αναπαράσταση των αριθμητικών σχέσεων σε ένα διάγραμμα με άξονες.
Γραφήματα Συναρτήσεων:
Τα γραφήματα είναι οπτικές αναπαραστάσεις των συναρτήσεων.
Αντιστοιχίες και Σχέσεις:
Οι γραφικές παραστάσεις επιτρέπουν την οπτικοποίηση των σχέσεων μεταξύ διαφορετικών μεταβλητών. Για παράδειγμα, ένα γραμμικό γράφημα δείχνει πώς μια ποσότητα αλλάζει σταθερά σε σχέση με μια άλλη, ενώ ένα μη γραμμικό γράφημα μπορεί να δείχνει πολύπλοκες σχέσεις, όπως καμπύλες ή παραβολές. Οι γραφικές παραστάσεις χρησιμοποιούνται για να μελετηθούν οι αντιστοιχίες μεταξύ διαφορετικών ποσοτήτων και να προβλεφθεί η συμπεριφορά συστημάτων.
Εφαρμογές στην Πραγματική Ζωή:
Ο καρτεσιανός λογισμός και τα γραφήματα έχουν αμέτρητες εφαρμογές στην καθημερινή ζωή και στην επιστήμη. Στη φυσική, χρησιμοποιούνται για να περιγράψουν την κίνηση των σωμάτων, τις δυνάμεις και τις ενεργειακές μεταβολές. Στην οικονομία, χρησιμοποιούνται για την ανάλυση των τάσεων της αγοράς, την προβολή κερδών και ζημιών και την πρόβλεψη της ανάπτυξης.
Η Επιστήμη των Γραφημάτων:
Η μελέτη των γραφημάτων είναι μια σημαντική πτυχή των μαθηματικών και της επιστήμης δεδομένων. Τα γραφήματα επιτρέπουν την ανάλυση δεδομένων, την αναγνώριση μοτίβων και την εξαγωγή συμπερασμάτων. Για παράδειγμα, ένα γράφημα μπορεί να χρησιμοποιηθεί για να παρακολουθεί την αύξηση ή μείωση μιας τιμής σε σχέση με το χρόνο, κάτι που είναι θεμελιώδες στην επιστημονική έρευνα και την επιχειρηματική ανάλυση.
Συμπέρασμα:
Ο καρτεσιανός λογισμός και τα γραφήματα είναι αναπόσπαστα κομμάτια της σύγχρονης μαθηματικής σκέψης και έχουν εφαρμογές σε πολλούς τομείς. Η δυνατότητα οπτικής αναπαράστασης μαθηματικών σχέσεων μέσω γραφημάτων προσφέρει μια ισχυρή μέθοδο για την ανάλυση και την κατανόηση σύνθετων φαινομένων, ενώ τα εργαλεία αυτά συνεχίζουν να είναι κρίσιμα για την επίλυση πρακτικών προβλημάτων και τη λήψη αποφάσεων.
Οι συντεταγμένες και οι συναρτήσεις είναι θεμελιώδεις έννοιες στη μαθηματική ανάλυση και τη γεωμετρία, παρέχοντας τα εργαλεία για την αναπαράσταση και την κατανόηση των σχέσεων μεταξύ μεταβλητών και γεωμετρικών σχημάτων. Η ανάπτυξη των Καρτεσιανών συντεταγμένων από τον René Descartes (Ρενέ Ντεκάρτ) υπήρξε ένα από τα πιο σημαντικά βήματα προς τη σύγχρονη γεωμετρία και την ανάλυση.
Καρτεσιανό Σύστημα Συντεταγμένων:
Το Καρτεσιανό σύστημα συντεταγμένων επιτρέπει την αναπαράσταση γεωμετρικών σχημάτων και μαθηματικών συναρτήσεων σε ένα επίπεδο ή σε έναν χώρο μέσω αριθμητικών τιμών.
Η Έννοια των Συναρτήσεων:
Μια συνάρτηση είναι μια μαθηματική σχέση που συνδέει κάθε τιμή από ένα σύνολο εισόδων (ονομάζεται πεδίο ορισμού) με ακριβώς μία τιμή σε ένα σύνολο εξόδων (ονομάζεται πεδίο τιμών). Οι συναρτήσεις είναι θεμελιώδεις για την κατανόηση των μαθηματικών σχέσεων και χρησιμοποιούνται για να περιγράψουν φυσικά φαινόμενα, οικονομικές συναλλαγές, και τεχνολογικές διαδικασίες.
Η Σύνδεση των Συναρτήσεων με το Καρτεσιανό Σύστημα:
Το Καρτεσιανό σύστημα συντεταγμένων επιτρέπει την αναπαράσταση των συναρτήσεων με γραφικές παραστάσεις
Η Επανάσταση του René Descartes:
Ο René Descartes, γνωστός και ως Καρτέσιος, έφερε επανάσταση στη γεωμετρία με την εισαγωγή των συντεταγμένων. Η εργασία του “La Géométrie” (1637) εισήγαγε την ιδέα της χρήσης αριθμών για την αναπαράσταση γεωμετρικών σχημάτων, μια ιδέα που αποτελεί το θεμέλιο της αναλυτικής γεωμετρίας. Η εισαγωγή του Καρτεσιανού συστήματος συντεταγμένων επιτρέπει στους μαθηματικούς να αναλύουν γεωμετρικά προβλήματα μέσω της άλγεβρας και των συναρτήσεων.
Εφαρμογές των Συντεταγμένων και των Συναρτήσεων:
Οι συντεταγμένες και οι συναρτήσεις έχουν αμέτρητες εφαρμογές σε πολλούς τομείς. Στη φυσική, χρησιμοποιούνται για να περιγράψουν την κίνηση των σωμάτων, την πορεία των βλημάτων, και την κατανομή των δυνάμεων. Στη μηχανική, οι συναρτήσεις χρησιμοποιούνται για τον σχεδιασμό μηχανημάτων και συστημάτων ελέγχου. Στην οικονομία, μοντέλα βασισμένα σε συναρτήσεις περιγράφουν τη συμπεριφορά των αγορών και την ανάπτυξη της οικονομίας.
Συμπέρασμα:
Οι συντεταγμένες και οι συναρτήσεις είναι από τα πιο θεμελιώδη εργαλεία στα μαθηματικά και την επιστήμη, επιτρέποντας την αναπαράσταση και την κατανόηση των σχέσεων μεταξύ μεταβλητών και γεωμετρικών σχημάτων. Η ανάπτυξη του Καρτεσιανού συστήματος συντεταγμένων από τον René Descartes αποτέλεσε μια από τις πιο σημαντικές προόδους στη μαθηματική σκέψη, με διαχρονική επιρροή σε πολλούς επιστημονικούς και τεχνολογικούς τομείς.
Ο μετασχηματισμός και η προβολή είναι κεντρικές έννοιες στη γεωμετρία και τα μαθηματικά, με εφαρμογές σε πολλούς τομείς, όπως η φυσική, η μηχανική, η τέχνη και η αρχιτεκτονική. Οι μετασχηματισμοί περιλαμβάνουν αλλαγές στην τοποθέτηση, το σχήμα ή το μέγεθος των γεωμετρικών σχημάτων, ενώ οι προβολές αναφέρονται στη διαδικασία αναπαράστασης τρισδιάστατων αντικειμένων σε δύο διαστάσεις.
Μετασχηματισμοί:
Οι μετασχηματισμοί είναι μαθηματικές διαδικασίες που αλλάζουν τη θέση ή το σχήμα ενός αντικειμένου. Μερικοί από τους πιο συνηθισμένους μετασχηματισμούς περιλαμβάνουν:
Μεταφορά: Μετατόπιση ενός αντικειμένου από μία θέση σε μια άλλη χωρίς να αλλάζει το σχήμα ή το μέγεθός του.
Περιστροφή: Περιστροφή ενός αντικειμένου γύρω από ένα σημείο ή έναν άξονα.
Ανάκλαση: Αναστροφή ενός αντικειμένου ως προς μια γραμμή (σε δύο διαστάσεις) ή ως προς ένα επίπεδο (σε τρεις διαστάσεις).
Διαστολή: Αλλαγή στο μέγεθος ενός αντικειμένου, με διατήρηση του σχήματός του.
Προβολές:
Οι προβολές είναι μια μέθοδος για τη δημιουργία ενός δισδιάστατου σχεδίου από ένα τρισδιάστατο αντικείμενο. Οι πιο κοινές προβολές περιλαμβάνουν:
Ορθογραφική προβολή: Χρησιμοποιείται για τη δημιουργία προβολών που διατηρούν τις πραγματικές διαστάσεις του αντικειμένου. Κάθε πλευρά του αντικειμένου προβάλλεται σε ένα επίπεδο κάθετα προς την επιφάνειά του.
Προοπτική προβολή: Χρησιμοποιείται για τη δημιουργία προβολών που μιμούνται τον τρόπο με τον οποίο το ανθρώπινο μάτι αντιλαμβάνεται τα αντικείμενα. Οι γραμμές που είναι παράλληλες στο πραγματικό αντικείμενο συγκλίνουν σε ένα σημείο στον ορίζοντα στο σχέδιο, δημιουργώντας την αίσθηση του βάθους.
Αναμορφώσεις και Μορφές στη Φύση:
Η φύση παρουσιάζει πολλά παραδείγματα μετασχηματισμών και αναμορφώσεων. Από την ανάπτυξη των φυτών και των ζώων έως τις μορφές που δημιουργούνται από τη ροή των υγρών, οι μετασχηματισμοί είναι παντού. Για παράδειγμα, τα κύματα του ωκεανού μετασχηματίζονται συνεχώς καθώς κινούνται προς την ακτή, και οι στροβιλισμοί στον αέρα και το νερό δημιουργούν πολύπλοκα γεωμετρικά μοτίβα.
Προβολές και Τέχνη:
Στην τέχνη, οι προβολές και οι αναμορφώσεις χρησιμοποιούνται για να δημιουργήσουν έργα που παίζουν με την προοπτική και την αντίληψη του χώρου. Οι καλλιτέχνες της Αναγέννησης, για παράδειγμα, ανέπτυξαν την τεχνική της προοπτικής για να δώσουν βάθος και ρεαλισμό στους πίνακές τους.
Εφαρμογές στη Μηχανική και την Αρχιτεκτονική:
Οι μετασχηματισμοί και οι προβολές είναι κρίσιμες για τη σχεδίαση και την κατασκευή κτηρίων, γεφυρών, και άλλων δομών. Οι μηχανικοί χρησιμοποιούν μαθηματικές μεθόδους για να υπολογίσουν τις μετασχηματιστικές δυνάμεις που δρουν σε ένα αντικείμενο, όπως η κάμψη και η παραμόρφωση, ενώ οι αρχιτέκτονες χρησιμοποιούν προβολές για να δημιουργήσουν σχέδια που απεικονίζουν πώς θα φαίνεται ένα κτήριο από διαφορετικές οπτικές γωνίες.
Συμπέρασμα:
Οι μετασχηματισμοί και οι προβολές είναι θεμελιώδεις έννοιες στα μαθηματικά και την επιστήμη, με ευρύ φάσμα εφαρμογών που εκτείνονται από τη φυσική και τη μηχανική έως την τέχνη και την αρχιτεκτονική. Κατανοώντας αυτές τις έννοιες, μπορούμε να αναλύσουμε και να ερμηνεύσουμε τον κόσμο γύρω μας, καθώς και να δημιουργήσουμε νέες δομές και έργα τέχνης που επηρεάζουν τον τρόπο που αντιλαμβανόμαστε το χώρο και το χρόνο.
Οι ομοιότητες, ή αλλιώς ομοθεσίες, και οι αντιστροφές είναι θεμελιώδεις γεωμετρικοί μετασχηματισμοί που διατηρούν τη δομή ενός σχήματος ενώ αλλάζουν το μέγεθος ή την κατεύθυνσή του. Αυτοί οι μετασχηματισμοί είναι κεντρικοί στη μελέτη των γεωμετρικών σχέσεων και έχουν ευρεία εφαρμογή στη μαθηματική ανάλυση και τη φυσική.
Ομοιότητα (Ομοθεσία):
Η ομοιότητα είναι ένας μετασχηματισμός που διατηρεί το σχήμα ενός αντικειμένου, αλλά αλλάζει το μέγεθός του. Σε μια ομοιότητα, οι γωνίες διατηρούνται ίδιες, ενώ οι αποστάσεις μεταξύ των σημείων του σχήματος πολλαπλασιάζονται με έναν σταθερό λόγο, που ονομάζεται συντελεστής ομοιότητας.
Ομοθεσία: Η ομοθεσία είναι μια ειδική περίπτωση ομοιότητας όπου όλα τα σημεία ενός σχήματος μετακινούνται κατά μήκος ευθειών που διέρχονται από ένα σταθερό σημείο (κέντρο της ομοθεσίας) και οι αποστάσεις από το κέντρο πολλαπλασιάζονται με έναν σταθερό λόγο. Ο συντελεστής αυτός καθορίζει αν το σχήμα θα μεγαλώσει (όταν ο λόγος είναι μεγαλύτερος από 1) ή θα μικρύνει (όταν ο λόγος είναι μικρότερος από 1). Η ομοιότητα είναι κρίσιμη για την κατανόηση της γεωμετρίας και χρησιμοποιείται ευρέως στην αρχιτεκτονική, τη μηχανική και τη φυσική, όπου συχνά χρειάζεται να μελετηθούν μοντέλα που είναι ομοιόμορφα σε κλίμακα με πραγματικά αντικείμενα.
Αντιστροφή:
Η αντιστροφή είναι ένας γεωμετρικός μετασχηματισμός που αντιστρέφει την κατεύθυνση των σημείων ως προς έναν κύκλο. Σε αυτόν τον μετασχηματισμό, ένα σημείο P έξω από τον κύκλο μετασχηματίζεται σε ένα νέο σημείο P′ μέσα στον κύκλο, τέτοιο ώστε το γινόμενο των αποστάσεων από το κέντρο του κύκλου να παραμένει σταθερό.
Αντίστροφη Σχέση: Μια αντιστροφή αλλάζει το προσανατολισμό ενός σχήματος και μπορεί να μετατρέψει κυκλικά σχήματα σε άλλα κυκλικά σχήματα ή σε ευθείες γραμμές, ανάλογα με τη θέση τους σε σχέση με τον κύκλο της αντιστροφής.
Η αντιστροφή είναι σημαντική στη γεωμετρική ανάλυση και στη θεωρία των μετασχηματισμών, και έχει εφαρμογές στην οπτική και τη μελέτη των συμμετρικών συστημάτων.
Εφαρμογές των Μετασχηματισμών:
Οι μετασχηματισμοί ομοιότητας και αντιστροφής είναι κρίσιμοι για τη μοντελοποίηση και την κατανόηση της συμμετρίας στη φύση και τη γεωμετρία. Οι αρχιτέκτονες και οι σχεδιαστές χρησιμοποιούν αυτούς τους μετασχηματισμούς για να δημιουργήσουν δομές που είναι αρμονικές και αισθητικά ευχάριστες. Στη φυσική, αυτοί οι μετασχηματισμοί χρησιμοποιούνται για να κατανοήσουν τα φαινόμενα που σχετίζονται με την κλίμακα, όπως η κίνηση των υγρών και των αερίων.
Συμπέρασμα:
Οι ομοιότητες και οι αντιστροφές είναι θεμελιώδεις έννοιες στη γεωμετρία που μας επιτρέπουν να κατανοήσουμε και να αναλύσουμε τη σχέση μεταξύ διαφορετικών γεωμετρικών σχημάτων και να διατηρήσουμε τη δομή τους ενώ αλλάζουμε το μέγεθος ή την κατεύθυνσή τους. Αυτές οι έννοιες είναι χρήσιμες τόσο στη θεωρητική μελέτη όσο και στις πρακτικές εφαρμογές, από την αρχιτεκτονική και τη μηχανική μέχρι τη φυσική και τα μαθηματικά.
«Τετραγωνίζοντας τον κύκλο» (30 λεπτά)
Τα πολύεδρα είναι γεωμετρικά σχήματα που αποτελούνται από επίπεδες επιφάνειες, οι οποίες ονομάζονται έδρες, και σχηματίζονται από πολυγωνικές πλευρές που ενώνονται κατά μήκος ακμών. Τα πολύεδρα είναι σημαντικά στη γεωμετρία και έχουν εφαρμογές σε πολλούς τομείς, όπως η αρχιτεκτονική, η χημεία και η πληροφορική.
Πλατωνικά Στερεά:
Τα πιο γνωστά πολύεδρα είναι τα πλατωνικά στερεά, τα οποία είναι τα μόνα πολύεδρα που έχουν όλες τις έδρες τους ίδιες κανονικές πολύγωνες και όλες τις γωνίες τους ίδιες. Υπάρχουν μόνο πέντε πλατωνικά στερεά:
Τετράεδρο: Έχει 4 έδρες, που είναι κανονικά τρίγωνα.
Κύβος (Εξάεδρο): Έχει 6 έδρες, που είναι τετράγωνα.
Οκτάεδρο: Έχει 8 έδρες, που είναι κανονικά τρίγωνα.
Δωδεκάεδρο: Έχει 12 έδρες, που είναι κανονικά πεντάγωνα.
Εικοσάεδρο: Έχει 20 έδρες, που είναι κανονικά τρίγωνα.
Το Θεώρημα του Euler:
Ένα από τα πιο σημαντικά αποτελέσματα στη μελέτη των πολυέδρων είναι το θεώρημα του Euler, το οποίο συνδέει τον αριθμό των κορυφών (VVV), των ακμών (EEE) και των εδρών (FFF) ενός πολύεδρου με μια απλή σχέση:
V−E+F=2V – E + F = 2V−E+F=2
Αυτό το θεώρημα ισχύει για όλα τα κυρτά πολύεδρα και είναι ένα θεμελιώδες αποτέλεσμα στη γεωμετρία των πολυέδρων. Το θεώρημα του Euler μας δίνει μια βαθιά κατανόηση της τοπολογικής δομής των πολυέδρων και χρησιμοποιείται για την ανάλυση της μορφής και της δομής τους.
Εφαρμογές των Πολυέδρων:
Τα πολύεδρα έχουν πολλές εφαρμογές στην καθημερινή ζωή και στις επιστήμες:
Αρχιτεκτονική και Σχεδιασμός: Τα πολύεδρα χρησιμοποιούνται στη σχεδίαση κτηρίων και άλλων κατασκευών λόγω της σταθερότητας και της αισθητικής τους.
Χημεία: Τα μόρια σε κρυσταλλικές δομές συχνά σχηματίζουν πολύεδρα, και η κατανόηση της γεωμετρίας τους είναι κρίσιμη για την κατανόηση των χημικών ιδιοτήτων.
Πληροφορική και Γραφικά: Στα τρισδιάστατα γραφικά και στον σχεδιασμό παιχνιδιών, τα πολύεδρα χρησιμοποιούνται για την αναπαράσταση και τη μοντελοποίηση τρισδιάστατων αντικειμένων.
Συμπέρασμα:
Τα πολύεδρα είναι βασικά σχήματα στη γεωμετρία που έχουν σημαντική θεωρητική και πρακτική σημασία. Το θεώρημα του Euler προσφέρει ένα απλό αλλά ισχυρό εργαλείο για την κατανόηση της δομής των πολυέδρων, ενώ τα πλατωνικά στερεά προσφέρουν μια ματιά στην ομορφιά και την αρμονία που μπορεί να βρεθεί στα γεωμετρικά σχήματα. Οι εφαρμογές των πολυέδρων εκτείνονται σε πολλούς τομείς, καθιστώντας τα κρίσιμα για την κατανόηση και τη διαμόρφωση του κόσμου γύρω μας.
Η γεωμετρία της καμπυλότητας είναι ένας τομέας που επεκτείνεται πέρα από την παραδοσιακή Ευκλείδεια γεωμετρία, και εξετάζει τις ιδιότητες των χώρων και των επιφανειών που δεν είναι απαραίτητα επίπεδες. Η κατανόηση της καμπυλότητας είναι κρίσιμη για την κατανόηση πολλών φυσικών και γεωμετρικών φαινομένων, όπως η γενική θεωρία της σχετικότητας και η μορφή του σύμπαντος.
Καμπυλότητα και Μη Ευκλείδειες Γεωμετρίες:
Σε έναν επίπεδο χώρο, η Ευκλείδεια γεωμετρία είναι πλήρως επαρκής για να περιγράψει τις σχέσεις μεταξύ σημείων, γραμμών και γωνιών. Ωστόσο, όταν ο χώρος είναι καμπύλος, οι Ευκλείδειες αρχές δεν ισχύουν πάντα. Η γεωμετρία της καμπυλότητας περιλαμβάνει την εξέταση χώρων με θετική, αρνητική ή μηδενική καμπυλότητα.
Σφαιρική Γεωμετρία: Σε μια επιφάνεια σφαίρας, όπως η επιφάνεια της Γης, οι γραμμές που αντιπροσωπεύουν τους συντομότερους δρόμους μεταξύ δύο σημείων (γεωδαισιακές γραμμές) είναι μέρη κύκλων (μεγάλοι κύκλοι). Στη σφαιρική γεωμετρία, το άθροισμα των γωνιών ενός τριγώνου είναι μεγαλύτερο από 180°.
Υπερβολική Γεωμετρία: Σε χώρους με αρνητική καμπυλότητα, όπως ένα υπερβολοειδές, οι γραμμές αποκλίνουν καθώς κινούνται μακριά η μία από την άλλη. Στην υπερβολική γεωμετρία, το άθροισμα των γωνιών ενός τριγώνου είναι μικρότερο από 180°.
Το Θεώρημα του Gauss και η Καμπυλότητα:
Το θεώρημα του Gauss, γνωστό και ως “θεώρημα egregium”, δηλώνει ότι η καμπυλότητα μιας επιφάνειας είναι μια εγγενής ιδιότητα που δεν αλλάζει όταν η επιφάνεια παραμορφώνεται χωρίς τέντωμα. Αυτό σημαίνει ότι η καμπυλότητα μπορεί να μετρηθεί και να υπολογιστεί αποκλειστικά με πληροφορίες που βρίσκονται πάνω στην επιφάνεια, χωρίς να χρειάζεται να εξεταστεί ο τρισδιάστατος χώρος στον οποίο είναι ενσωματωμένη. Εφαρμογές της Καμπυλότητας:
Η κατανόηση της καμπυλότητας είναι απαραίτητη για τη γενική θεωρία της σχετικότητας του Einstein, όπου η καμπυλότητα του χωροχρόνου προκαλείται από την παρουσία μάζας και ενέργειας. Η γεωμετρία της καμπυλότητας εφαρμόζεται επίσης στην αστρονομία, στη μελέτη των γαλαξιών και στη σχεδίαση γεφυρών και άλλων δομών που απαιτούν γνώση της στατικής και δυναμικής καμπυλών επιφανειών.
Συμπέρασμα:
Η γεωμετρία της καμπυλότητας ανοίγει ένα παράθυρο σε έναν κόσμο πέρα από την Ευκλείδεια γεωμετρία, επιτρέποντας την κατανόηση και την ανάλυση χώρων και επιφανειών με καμπυλότητα. Οι εφαρμογές της καμπυλότητας είναι διάχυτες στην επιστήμη και την τεχνολογία, κάνοντάς την μια κρίσιμη έννοια για την κατανόηση του κόσμου και του σύμπαντος.
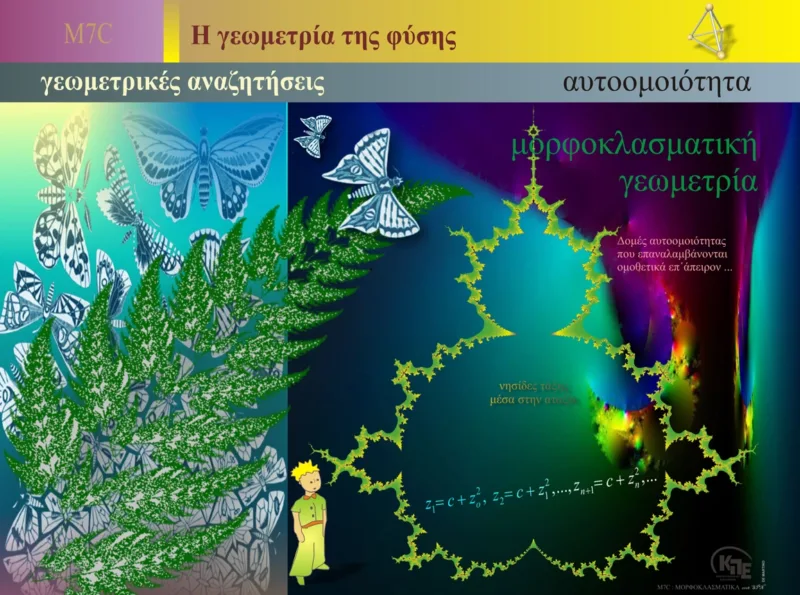
Η μορφοκλασματική γεωμετρία (ή φράκταλ γεωμετρία) είναι ένας κλάδος των μαθηματικών που εξετάζει γεωμετρικά σχήματα με πολύπλοκη, αυτοόμοια δομή, η οποία επαναλαμβάνεται σε διαφορετικές κλίμακες. Αυτά τα σχήματα είναι γνωστά ως φράκταλ, και η εμφάνισή τους είναι ευρέως διαδεδομένη στη φύση, καθώς και σε διάφορους τομείς της επιστήμης και της τέχνης.
Αυτοομοιότητα:
Η βασική ιδιότητα των φράκταλ είναι η αυτοομοιότητα, δηλαδή η ιδιότητα ενός σχήματος να είναι παρόμοιο με τον εαυτό του όταν παρατηρείται σε διαφορετικές κλίμακες. Ένα φράκταλ μπορεί να έχει πολύπλοκες λεπτομέρειες, και αυτές οι λεπτομέρειες να επαναλαμβάνονται σε μικρότερες κλίμακες, σχεδόν επ’ άπειρον.
Παραδείγματα Αυτοομοιότητας στη Φύση: Ένα από τα πιο χαρακτηριστικά παραδείγματα αυτοομοιότητας στη φύση είναι οι φτέρες, των οποίων τα φύλλα έχουν παρόμοια δομή με το συνολικό φυτό, αλλά σε μικρότερη κλίμακα. Το ίδιο συμβαίνει και με τις ακτές των ποταμών, τις νιφάδες χιονιού, και τα κοχύλια.
Φράκταλ στη Φύση και την Τέχνη:
Η μορφοκλασματική γεωμετρία δεν είναι απλώς μια μαθηματική θεωρία, αλλά και μια έννοια που εφαρμόζεται ευρέως στη φύση και στην τέχνη. Τα φράκταλ μπορούν να χρησιμοποιηθούν για τη μοντελοποίηση σύνθετων φυσικών φαινομένων, όπως τα σύννεφα, οι ακτογραμμές, και οι κεραυνοί.
Στην τέχνη, τα φράκταλ έχουν εμπνεύσει καλλιτέχνες να δημιουργήσουν έργα με πολύπλοκα και επαναλαμβανόμενα μοτίβα που προσομοιάζουν τις δομές που παρατηρούνται στη φύση. Αυτή η μορφολογία συχνά αναφέρεται ως “φυσική τέχνη” και χρησιμοποιείται για να δημιουργήσει οπτικά εφέ που είναι τόσο εντυπωσιακά όσο και καθηλωτικά.
Εφαρμογές της Μορφοκλασματικής Γεωμετρίας:
Οι εφαρμογές της μορφοκλασματικής γεωμετρίας εκτείνονται από την επιστήμη μέχρι την τεχνολογία:
Γεωγραφία: Χρησιμοποιείται για τη μοντελοποίηση και ανάλυση γεωλογικών και γεωγραφικών φαινομένων, όπως η διάβρωση των ακτών και η διαμόρφωση των ποταμών.
Ιατρική: Χρησιμοποιείται για τη μελέτη των αγγειακών συστημάτων και άλλων δομών του σώματος που παρουσιάζουν φράκταλ συμπεριφορά.
Οικονομία: Εφαρμόζεται στη μελέτη των αγορών, όπου οι φράκταλ δομές μπορούν να βοηθήσουν στην ανάλυση της αστάθειας των τιμών.
Συμπέρασμα:
Η μορφοκλασματική γεωμετρία παρέχει ένα ισχυρό εργαλείο για την κατανόηση και την περιγραφή των σύνθετων και επαναλαμβανόμενων δομών που εμφανίζονται τόσο στη φύση όσο και σε ανθρώπινα δημιουργήματα. Η αυτοομοιότητα και η πολύπλοκη δομή των φράκταλ προκαλούν δέος και έχουν σημαντικές εφαρμογές σε πολλούς τομείς, επιτρέποντας μια βαθύτερη κατανόηση της φυσικής και γεωμετρικής ομορφιάς που μας περιβάλλει.
«Ρουά ματ» (80 λεπτά)
Η θεωρία παιγνίων και οι στρατηγικοί σχεδιασμοί είναι κλάδοι των μαθηματικών που ασχολούνται με την ανάλυση καταστάσεων όπου η έκβαση εξαρτάται από τις αποφάσεις που λαμβάνουν πολλά άτομα ή “παίκτες”. Σε τέτοιες καταστάσεις, κάθε παίκτης προσπαθεί να μεγιστοποιήσει το όφελός του, λαμβάνοντας υπόψη τις αποφάσεις των άλλων παικτών.
Θεωρία Παιγνίων:
Η θεωρία παιγνίων αναπτύχθηκε ως κλάδος των μαθηματικών και της οικονομικής θεωρίας, και επικεντρώνεται στη μοντελοποίηση στρατηγικών αλληλεπιδράσεων μεταξύ ορθολογικών ληπτών αποφάσεων. Κάθε παίγνιο αποτελείται από έναν καθορισμένο αριθμό παικτών, κάθε ένας από τους οποίους επιλέγει μια στρατηγική. Η έκβαση του παιγνίου καθορίζεται από τον συνδυασμό των στρατηγικών που επιλέγουν όλοι οι παίκτες.
Τύποι Παιγνίων:
Μηδενικού αθροίσματος παίγνια: Σε αυτά τα παίγνια, το συνολικό όφελος που αποκομίζουν όλοι οι παίκτες μαζί είναι μηδενικό. Αυτό σημαίνει ότι το κέρδος ενός παίκτη ισοδυναμεί με τη ζημία ενός άλλου. Ένα κλασικό παράδειγμα είναι το σκάκι, όπου η νίκη ενός παίκτη συνεπάγεται την ήττα του άλλου.
Μη μηδενικού αθροίσματος παίγνια: Σε αυτά τα παίγνια, η συνολική έκβαση μπορεί να ωφελήσει όλους τους παίκτες ή να επιφέρει ζημία σε όλους, ανάλογα με τις στρατηγικές τους. Ένα παράδειγμα είναι οι διαπραγματεύσεις, όπου η συνεργασία μπορεί να οδηγήσει σε αμοιβαίο κέρδος.
Κλασικά Παίγνια:
Το δίλημμα του φυλακισμένου: Πρόκειται για ένα κλασικό πρόβλημα στη θεωρία παιγνίων που δείχνει πώς η αβεβαιότητα και η έλλειψη εμπιστοσύνης μπορούν να οδηγήσουν σε ένα λιγότερο ευνοϊκό αποτέλεσμα. Στο σενάριο αυτό, δύο φυλακισμένοι πρέπει να επιλέξουν αν θα προδώσουν ο ένας τον άλλον ή θα συνεργαστούν. Αν και η συνεργασία αποφέρει το καλύτερο συνολικό αποτέλεσμα, ο φόβος της προδοσίας μπορεί να οδηγήσει και τους δύο στην προδοσία, με αποτέλεσμα μια λιγότερο επιθυμητή έκβαση.
Το παίγνιο του κοτόπουλου: Σε αυτό το παίγνιο, δύο οδηγοί κατευθύνονται ο ένας προς τον άλλον σε ένα στενό δρόμο. Ο πρώτος που θα στρίψει για να αποφύγει τη σύγκρουση θεωρείται “κοτόπουλο” και χάνει το παιχνίδι. Το παίγνιο αυτό χρησιμοποιείται συχνά για να περιγράψει καταστάσεις όπου δύο μέρη είναι σε σύγκρουση και καμία πλευρά δεν θέλει να υποχωρήσει.
Στρατηγικές και Γράφοι:
Οι στρατηγικές που μπορούν να χρησιμοποιήσουν οι παίκτες σε ένα παίγνιο αναλύονται συχνά με τη χρήση μαθηματικών εργαλείων όπως οι γράφοι. Οι γράφοι μπορούν να αναπαραστήσουν τις επιλογές στρατηγικής των παικτών και τις σχέσεις μεταξύ τους. Μέσω των γράφων, μπορούν να αναλυθούν οι σταθερές καταστάσεις ενός παιγνίου, γνωστές ως ισορροπία Nash, όπου κανένας παίκτης δεν έχει κίνητρο να αλλάξει τη στρατηγική του αν δεν αλλάξουν και οι υπόλοιποι παίκτες.
Μαθηματική Προσδοκία και Ορθολογικές Αποφάσεις:
Η μαθηματική προσδοκία είναι ένα κρίσιμο εργαλείο στη λήψη αποφάσεων. Υπολογίζοντας την αναμενόμενη τιμή των εκβάσεων βάσει των πιθανοτήτων τους, οι παίκτες μπορούν να επιλέξουν τη στρατηγική που μεγιστοποιεί την αναμενόμενη απόδοση. Αυτός ο υπολογισμός παίζει σημαντικό ρόλο στην ανάλυση κινδύνου και στη στρατηγική λήψη αποφάσεων.
Εφαρμογές:
Οικονομικά: Η θεωρία παιγνίων χρησιμοποιείται για την κατανόηση των ανταγωνιστικών αγορών, της τιμολόγησης, και των στρατηγικών πωλήσεων.
Πολιτική: Αναλύει τις αλληλεπιδράσεις μεταξύ κρατών, όπως στις διαπραγματεύσεις, τις συμμαχίες και τις συγκρούσεις.
Ψυχολογία: Χρησιμοποιείται για να μελετηθεί η ανθρώπινη συμπεριφορά, οι στρατηγικές επιλογές, και η λήψη αποφάσεων υπό πίεση.
Βιολογία: Εφαρμόζεται στη μελέτη της εξέλιξης, της συνεργασίας και του ανταγωνισμού μεταξύ ειδών.
Συμπέρασμα:
Η θεωρία παιγνίων και οι στρατηγικοί σχεδιασμοί παρέχουν σημαντικά εργαλεία για την κατανόηση της λήψης αποφάσεων σε πολύπλοκες και αλληλεπιδραστικές καταστάσεις. Μέσω αυτών, μπορούμε να κατανοήσουμε καλύτερα την ανθρώπινη συμπεριφορά, να βελτιώσουμε τις διαπραγματεύσεις και να αναπτύξουμε στρατηγικές που οδηγούν σε πιο επιθυμητά αποτελέσματα, τόσο σε προσωπικό όσο και σε επαγγελματικό επίπεδο.
Η στρατηγική ανάλυση και η θεωρία παιγνίων είναι κρίσιμες για την κατανόηση και την επίλυση καταστάσεων σύγκρουσης, όπου οι αποφάσεις που λαμβάνει κάθε πλευρά επηρεάζουν τα αποτελέσματα για όλες τις εμπλεκόμενες πλευρές. Αυτές οι θεωρίες βοηθούν στη μελέτη της δυναμικής των συγκρούσεων και στη λήψη αποφάσεων που οδηγούν σε στρατηγικά πλεονεκτήματα.
Θεωρία Παιγνίων και Στρατηγική Ανάλυση:
Η θεωρία παιγνίων αναλύει τις στρατηγικές επιλογές που λαμβάνονται σε ένα πλαίσιο όπου πολλοί “παίκτες” ή παράγοντες αλληλεπιδρούν. Η στρατηγική ανάλυση περιλαμβάνει τη μελέτη των αποφάσεων που πρέπει να ληφθούν από κάθε παίκτη προκειμένου να επιτύχει το καλύτερο δυνατό αποτέλεσμα, λαμβάνοντας υπόψη τις πιθανές αποφάσεις των άλλων παικτών.
Ισορροπία Nash: Ένα από τα πιο σημαντικά αποτελέσματα στη θεωρία παιγνίων είναι η έννοια της ισορροπίας Nash, που εισήγαγε ο μαθηματικός John Nash. Μια κατάσταση είναι ισορροπία Nash όταν κανένας παίκτης δεν μπορεί να βελτιώσει το αποτέλεσμα για τον εαυτό του αλλάζοντας μονομερώς τη στρατηγική του. Η ισορροπία αυτή παρέχει μια σταθερή λύση σε καταστάσεις σύγκρουσης, όπου οι παίκτες έχουν αντικρουόμενα συμφέροντα.
Στρατηγικά Παιχνίδια και Σύγκρουση:
Στρατηγικά παιχνίδια: Τα στρατηγικά παιχνίδια αναπαριστούν καταστάσεις όπου οι παίκτες πρέπει να επιλέξουν μια στρατηγική με βάση τις επιλογές των άλλων. Σε αυτά τα παιχνίδια, κάθε παίκτης προσπαθεί να βρει τη βέλτιστη στρατηγική του λαμβάνοντας υπόψη τις πιθανές στρατηγικές των αντιπάλων.
Παραδείγματα Στρατηγικών Παιχνιδιών: Ένα παράδειγμα στρατηγικού παιχνιδιού είναι η ναυμαχία, όπου δύο πλευρές πρέπει να αποφασίσουν πού να τοποθετήσουν τα πλοία τους και πού να επιτεθούν. Η επιλογή της στρατηγικής εξαρτάται από το πώς εκτιμά ο καθένας τις κινήσεις του αντιπάλου.
Στρατηγική Ανάλυση στη Στρατιωτική Στρατηγική:
Η στρατηγική ανάλυση έχει ευρύτατες εφαρμογές στη στρατιωτική στρατηγική, όπου η κατανόηση των δυναμικών σύγκρουσης είναι ζωτικής σημασίας για την ανάπτυξη πλεονεκτικών θέσεων.
Υποβρύχια και Αεροπορική Κυριαρχία: Η ανάλυση της στρατηγικής τοποθέτησης υποβρυχίων και αεροπορικών δυνάμεων βασίζεται σε μοντέλα θεωρίας παιγνίων που λαμβάνουν υπόψη τις αλληλεπιδράσεις μεταξύ των δυνάμεων και την προσπάθεια ελαχιστοποίησης των απωλειών ενώ μεγιστοποιείται το πλεονέκτημα έναντι του αντιπάλου.
Στρατηγικές Θέσεις και Επιθέσεις: Η επιλογή των σημείων επίθεσης ή άμυνας βασίζεται σε μοντέλα που εξετάζουν το πώς κάθε ενέργεια μπορεί να επηρεάσει το συνολικό αποτέλεσμα της σύγκρουσης. Η στρατηγική ανάλυση βοηθά στον προσδιορισμό των κρίσιμων σημείων και στη λήψη αποφάσεων που ελαχιστοποιούν τον κίνδυνο και μεγιστοποιούν το όφελος.
Εφαρμογές σε Διάφορους Τομείς:
Πολιτική και Διεθνείς Σχέσεις: Η στρατηγική ανάλυση χρησιμοποιείται για την κατανόηση των διαπραγματεύσεων και των διπλωματικών συγκρούσεων μεταξύ κρατών, όπου κάθε πλευρά προσπαθεί να διαπραγματευτεί την καλύτερη δυνατή συμφωνία λαμβάνοντας υπόψη τις αντιδράσεις των άλλων κρατών.
Επιχειρήσεις και Διαχείριση: Οι επιχειρηματικές αποφάσεις συχνά λαμβάνονται με βάση τη στρατηγική ανάλυση της αγοράς και των ανταγωνιστών, προκειμένου να διασφαλιστεί ένα πλεονέκτημα έναντι των ανταγωνιστών.
Ψυχολογία και Ανθρώπινες Σχέσεις: Η κατανόηση των στρατηγικών αλληλεπιδράσεων μπορεί να βοηθήσει στην επίλυση συγκρούσεων και στη βελτίωση των σχέσεων μέσω της ανάλυσης των κινήτρων και των στόχων των εμπλεκόμενων μερών.
Συμπέρασμα:
Η στρατηγική ανάλυση είναι ένα ισχυρό εργαλείο που επιτρέπει την κατανόηση και την πρόβλεψη της συμπεριφοράς σε καταστάσεις σύγκρουσης και ανταγωνισμού. Μέσω της θεωρίας παιγνίων και της ανάλυσης στρατηγικών, οι μαθηματικοί, οι στρατηγικοί αναλυτές και οι επαγγελματίες μπορούν να αναπτύξουν στρατηγικές που ελαχιστοποιούν τον κίνδυνο και μεγιστοποιούν το όφελος, ανεξαρτήτως του πεδίου εφαρμογής.
Η στρατηγική στη θεωρία παιγνίων και στις διάφορες μορφές λήψης αποφάσεων είναι ένα σημαντικό πεδίο που εξετάζει την αλληλεπίδραση μεταξύ παικτών σε καταστάσεις όπου το αποτέλεσμα εξαρτάται από τις αποφάσεις όλων των εμπλεκομένων. Οι παίκτες μπορεί να βρεθούν αντιμέτωποι με την επιλογή ανάμεσα σε σύγκρουση και συμμαχία, και οι στρατηγικές τους αποφάσεις καθορίζουν όχι μόνο το αποτέλεσμα για τους ίδιους, αλλά και για τους υπόλοιπους παίκτες.
Στρατηγική Ανάλυση σε Παιχνίδια:
Τα παιχνίδια, όπως το σκάκι, χρησιμοποιούνται συχνά ως παραδείγματα στη θεωρία παιγνίων για να κατανοηθεί πώς οι στρατηγικές αποφάσεις επηρεάζουν το τελικό αποτέλεσμα. Στο σκάκι, κάθε κίνηση είναι κρίσιμη και κάθε παίκτης πρέπει να λαμβάνει υπόψη του την αντίδραση του αντιπάλου. Οι παίκτες μπορούν να επιλέξουν είτε να επιτεθούν (σύγκρουση) είτε να αμυνθούν (συμμαχία), και αυτές οι στρατηγικές επιλογές οδηγούν σε διαφορετικά αποτελέσματα.
Σύγκρουση ή Συμμαχία:
Ένα κεντρικό ερώτημα στη στρατηγική ανάλυση είναι αν οι παίκτες θα επιλέξουν τη σύγκρουση ή τη συμμαχία. Σε πολλές καταστάσεις, οι παίκτες μπορεί να κερδίσουν περισσότερα μέσω της συνεργασίας παρά μέσω της σύγκρουσης, αλλά η αβεβαιότητα και η έλλειψη εμπιστοσύνης συχνά οδηγούν σε συγκρουσιακές στρατηγικές.
Σύγκρουση: Η επιλογή της σύγκρουσης συνεπάγεται τον ανταγωνισμό μεταξύ των παικτών, όπου κάθε παίκτης προσπαθεί να μεγιστοποιήσει το δικό του όφελος εις βάρος των άλλων. Αυτή η στρατηγική μπορεί να οδηγήσει σε ένα ασταθές αποτέλεσμα όπου η ισορροπία είναι δύσκολο να επιτευχθεί.
Συμμαχία: Η επιλογή της συμμαχίας βασίζεται στη συνεργασία μεταξύ των παικτών για την επίτευξη ενός κοινού στόχου. Αυτή η στρατηγική μπορεί να οδηγήσει σε πιο σταθερά και αποδοτικά αποτελέσματα, αλλά απαιτεί εμπιστοσύνη και συντονισμό.
Στρατηγικά Παίγνια και Γράφοι:
Η στρατηγική ανάλυση περιλαμβάνει τη χρήση γραφημάτων για την αναπαράσταση των δυνατοτήτων κάθε παίκτη και των πιθανών εκβάσεων. Οι γράφοι αυτοί βοηθούν στον προσδιορισμό της βέλτιστης στρατηγικής και στην κατανόηση των σχέσεων μεταξύ των παικτών.
Εξαμερές Σκάκι: Στην ανάλυση στρατηγικών παιγνίων, συχνά χρησιμοποιούνται παραλλαγές του κλασικού σκακιού, όπως το εξαμερές σκάκι, για να εξεταστούν οι διαφορετικές στρατηγικές και οι επιπτώσεις τους. Σε αυτά τα παιχνίδια, οι παίκτες μπορούν να επιλέξουν στρατηγικές που ποικίλουν ανάλογα με τις σχέσεις και τις δυναμικές των άλλων παικτών.
Η Απόφαση και τα Μαθηματικά της Στρατηγικής:
Η λήψη απόφασης είναι ένα κρίσιμο σημείο σε οποιοδήποτε στρατηγικό παίγνιο. Οι παίκτες πρέπει να λάβουν υπόψη τους πιθανότητες, κινδύνους, και τις πιθανές ενέργειες των άλλων παικτών. Οι μαθηματικές μέθοδοι, όπως η θεωρία παιγνίων, χρησιμοποιούνται για να υπολογιστούν οι βέλτιστες στρατηγικές και να διασφαλιστεί ότι η επιλογή που γίνεται μεγιστοποιεί το όφελος του παίκτη.
Συμπέρασμα:
Η στρατηγική ανάλυση και η θεωρία παιγνίων παρέχουν εργαλεία για την κατανόηση της λήψης αποφάσεων σε καταστάσεις όπου υπάρχουν πολλοί εμπλεκόμενοι με αντικρουόμενα ή συγκλινόμενα συμφέροντα. Η σύγκρουση και η συμμαχία είναι δύο κύριες στρατηγικές επιλογές που επηρεάζουν το τελικό αποτέλεσμα, και η ικανότητα να κατανοηθούν αυτές οι επιλογές και να αναπτυχθούν βέλτιστες στρατηγικές είναι κρίσιμη για την επίτευξη επιτυχίας σε ένα ανταγωνιστικό περιβάλλον.
Η θεωρία της πιθανότητας και η λογική της τύχης αποτελούν βασικούς πυλώνες στα μαθηματικά και τη στατιστική, που μας βοηθούν να κατανοήσουμε και να αναλύσουμε φαινόμενα αβεβαιότητας. Οι έννοιες της τύχης και της πρόβλεψης είναι θεμελιώδεις για την κατανόηση παιχνιδιών τύχης, φυσικών φαινομένων και τη λήψη αποφάσεων σε καταστάσεις αβεβαιότητας.
Η Λογική της Τύχης:
Η τύχη συχνά συνδέεται με γεγονότα που δεν μπορούν να προβλεφθούν με ακρίβεια. Ωστόσο, μέσω της θεωρίας της πιθανότητας, μπορούμε να προσδιορίσουμε τις πιθανότητες εμφάνισης διαφόρων γεγονότων, ακόμα και αν τα συγκεκριμένα αποτελέσματα είναι απρόβλεπτα. Η λογική της τύχης αναπτύχθηκε για να μοντελοποιήσει και να ποσοτικοποιήσει αυτά τα φαινόμενα.
Πιθανότητα: Η πιθανότητα ενός γεγονότος είναι ένας αριθμός μεταξύ 0 και 1, που εκφράζει την πιθανότητα εμφάνισης του συγκεκριμένου γεγονότος. Ένα γεγονός με πιθανότητα 1 είναι βέβαιο, ενώ ένα γεγονός με πιθανότητα 0 είναι αδύνατο.
Στατιστική Ανάλυση: Η στατιστική αναλύει τα δεδομένα που σχετίζονται με τυχαία γεγονότα και μας επιτρέπει να κάνουμε προβλέψεις για μελλοντικά γεγονότα, με βάση παρελθόντα δεδομένα. Η στατιστική χρησιμοποιείται ευρέως σε τομείς όπως οι επιστήμες υγείας, η οικονομία και η κοινωνιολογία.
Παιχνίδια της Τύχης:
Τα παιχνίδια της τύχης, όπως τα ζάρια και το πόκερ, βασίζονται στην πιθανότητα και την τυχαιότητα. Αυτά τα παιχνίδια είναι συχνά παραδείγματα που χρησιμοποιούνται για να εξηγήσουν τις έννοιες της πιθανότητας.
Ζάρια: Στα ζάρια, κάθε πλευρά έχει την ίδια πιθανότητα εμφάνισης (1/6 για ένα κανονικό εξάεδρο ζάρι). Η πρόβλεψη του αποτελέσματος μιας ρίψης ζαριού είναι αδύνατη, αλλά η πιθανότητα εμφάνισης ενός συγκεκριμένου αριθμού μπορεί να υπολογιστεί με ακρίβεια.
Κέρμα: Στη ρίψη ενός κέρματος, υπάρχουν δύο δυνατά αποτελέσματα, «κορώνα» ή «γράμματα», με πιθανότητα 1/2 για το καθένα, εφόσον το κέρμα είναι ισορροπημένο.
Κάρτες: Στα παιχνίδια με τράπουλα, η πιθανότητα να τραβηχτεί μια συγκεκριμένη κάρτα από ένα πλήρες κατάστρωμα 52 καρτών μπορεί να υπολογιστεί με τη χρήση βασικών αρχών της θεωρίας της πιθανότητας. Για παράδειγμα, η πιθανότητα να τραβήξετε έναν άσο είναι 4/52 ή 1/13.
Ιστορική Ανάπτυξη:
Η θεωρία της πιθανότητας άρχισε να αναπτύσσεται τον 17ο αιώνα, όταν μαθηματικοί όπως ο Pierre de Fermat και ο Blaise Pascal άρχισαν να ασχολούνται με προβλήματα που σχετίζονταν με τα παιχνίδια της τύχης. Αργότερα, οι συνεισφορές άλλων μαθηματικών, όπως ο Pierre-Simon Laplace, βοήθησαν στην επέκταση της θεωρίας και στην εφαρμογή της σε μια ευρεία ποικιλία πεδίων.
Εφαρμογές της Πιθανότητας:
Η θεωρία της πιθανότητας έχει πολλές εφαρμογές στην καθημερινή ζωή και την επιστήμη:
Ασφάλεια και Ασφάλιση: Οι ασφαλιστικές εταιρείες χρησιμοποιούν την πιθανότητα για να υπολογίσουν τον κίνδυνο και να καθορίσουν τα ασφάλιστρα.
Οικονομία: Οι οικονομολόγοι χρησιμοποιούν την πιθανότητα για να αναλύσουν και να προβλέψουν την πορεία των χρηματαγορών και των επενδύσεων.
Υγεία: Οι γιατροί και οι ερευνητές χρησιμοποιούν στατιστικές πιθανότητες για να αξιολογήσουν την αποτελεσματικότητα των θεραπειών και να προβλέψουν την εξέλιξη ασθενειών.
Συμπέρασμα:
Η θεωρία της πιθανότητας μας δίνει τη δυνατότητα να αντιμετωπίζουμε την αβεβαιότητα με λογικό τρόπο, προσφέροντάς μας τα εργαλεία για να ποσοτικοποιούμε την τυχαιότητα και να λαμβάνουμε τεκμηριωμένες αποφάσεις. Στα παιχνίδια της τύχης, η κατανόηση της πιθανότητας είναι κρίσιμη για τη λήψη στρατηγικών αποφάσεων, αλλά οι εφαρμογές της εκτείνονται πολύ πέρα από το πλαίσιο των παιχνιδιών, επηρεάζοντας όλους τους τομείς της ανθρώπινης ζωής.
Η θεωρία των πιθανοτήτων ασχολείται με την ανάλυση και την περιγραφή των τυχαίων φαινομένων, και οι κατανομές της τύχης αποτελούν κεντρικό μέρος αυτής της θεωρίας. Μέσω της κατανόησης των κατανομών της τύχης, μπορούμε να περιγράψουμε πώς τα τυχαία γεγονότα κατανέμονται και να προβλέψουμε τα πιθανά αποτελέσματα.
Νόμος των Μεγάλων Αριθμών και Κατανομές:
Ο νόμος των μεγάλων αριθμών είναι ένα από τα βασικά θεωρήματα στην πιθανότητα. Σύμφωνα με αυτόν, καθώς το μέγεθος του δείγματος αυξάνεται, ο μέσος όρος των αποτελεσμάτων από τις επαναλαμβανόμενες δοκιμές θα πλησιάσει τη θεωρητική μέση τιμή. Αυτός ο νόμος εξηγεί γιατί, για παράδειγμα, αν ρίξετε ένα νόμισμα αρκετές φορές, το ποσοστό των κορώνα και γράμματα θα πλησιάσει το 50%.
Διωνυμική Κατανομή:
Η διωνυμική κατανομή είναι μια από τις πιο βασικές και σημαντικές κατανομές στην θεωρία πιθανοτήτων. Περιγράφει τον αριθμό επιτυχιών σε μια σειρά ανεξάρτητων και ίσων πιθανοτήτων δοκιμών, όπως π.χ. το πόσες φορές θα εμφανιστεί κορώνα σε 10 ρίψεις ενός νομίσματος.
Κατανομή Bernoulli:
Η κατανομή Bernoulli είναι μια ειδική περίπτωση της διωνυμικής κατανομής, όπου υπάρχει μόνο μία δοκιμή. Είναι η πιο απλή κατανομή πιθανότητας και χρησιμοποιείται για να περιγράψει φαινόμενα που έχουν δύο δυνατά αποτελέσματα, όπως η ρίψη ενός νομίσματος.
Γεωμετρική και Υπεργεωμετρική Κατανομή:
Γεωμετρική κατανομή: Περιγράφει τον αριθμό των ανεπιτυχών δοκιμών που απαιτούνται πριν από την πρώτη επιτυχία. Για παράδειγμα, εάν προσπαθείτε να ρίξετε ένα ζάρι και να φέρετε 6, η γεωμετρική κατανομή περιγράφει πόσες φορές θα χρειαστεί να ρίξετε το ζάρι μέχρι να πετύχετε το 6.
Υπεργεωμετρική κατανομή: Χρησιμοποιείται όταν οι δοκιμές δεν είναι ανεξάρτητες. Ένα παράδειγμα είναι η επιλογή καρτών από μια τράπουλα χωρίς επανατοποθέτηση. Η υπεργεωμετρική κατανομή περιγράφει την πιθανότητα να επιλέξετε έναν συγκεκριμένο αριθμό επιτυχιών (π.χ. άσους) από ένα περιορισμένο δείγμα.
Η Καμπύλη της Κανονικής Κατανομής:
Η κανονική κατανομή, γνωστή και ως κατανομή Gauss, είναι μια από τις πιο σημαντικές κατανομές στην θεωρία πιθανοτήτων. Περιγράφεται από την καμπύλη της καμπάνας και χρησιμοποιείται για να περιγράψει πολλές φυσικές και κοινωνικές φαινόμενα. Η κατανομή αυτή έχει ιδιαίτερη σημασία επειδή πολλές τυχαίες μεταβλητές τείνουν να είναι κανονικά κατανεμημένες όταν το μέγεθος του δείγματος είναι μεγάλο, λόγω του κεντρικού οριακού θεωρήματος.
Εφαρμογές των Κατανομών της Τύχης:
Στατιστική ανάλυση: Οι κατανομές χρησιμοποιούνται για την ανάλυση δεδομένων και την πραγματοποίηση προβλέψεων σε πολλούς τομείς, όπως τα οικονομικά, οι επιστήμες υγείας και η μηχανική.
Ασφάλιση: Οι ασφαλιστικές εταιρείες χρησιμοποιούν τις κατανομές για να υπολογίσουν τον κίνδυνο και να διαμορφώσουν τα ασφάλιστρα.
Τυχερά παιχνίδια: Στα τυχερά παιχνίδια, οι κατανομές της τύχης βοηθούν να κατανοηθούν οι πιθανότητες νίκης και να αναπτυχθούν στρατηγικές για τη βελτιστοποίηση των κερδών.
Συμπέρασμα:
Η κατανόηση των κατανομών της τύχης είναι θεμελιώδης για την ανάλυση των τυχαίων φαινομένων και την ποσοτικοποίηση της αβεβαιότητας. Μέσω των κατανομών, μπορούμε να περιγράψουμε πώς κατανέμονται τα τυχαία γεγονότα και να κάνουμε προβλέψεις που βασίζονται σε στατιστικά μοντέλα, με εφαρμογές που εκτείνονται από την οικονομία και την επιστήμη μέχρι τα καθημερινά προβλήματα.
Η τύχη και η πιθανότητα είναι έννοιες που συχνά φαίνονται να βρίσκονται σε αντίθεση με τη λογική και την αιτιοκρατία, αλλά στην πραγματικότητα, συνδέονται στενά μέσω των μαθηματικών και της στατιστικής. Η θεωρία των πιθανοτήτων προσπαθεί να ποσοτικοποιήσει την τύχη, να προβλέψει τα πιθανά αποτελέσματα τυχαίων γεγονότων και να κατανοήσει τα απρόβλεπτα φαινόμενα.
Πιθανό και Απρόβλεπτο:
Στην καθημερινή ζωή, τα τυχαία γεγονότα είναι συχνά απρόβλεπτα, όπως η ρίψη ενός νομίσματος ή η επιλογή ενός τυχαίου αριθμού. Ωστόσο, μέσω της θεωρίας των πιθανοτήτων, μπορούμε να προσδιορίσουμε τις πιθανότητες αυτών των γεγονότων και να κατανοήσουμε τα πιθανά αποτελέσματα. Αυτό σημαίνει ότι, αν και τα μεμονωμένα γεγονότα μπορεί να είναι απρόβλεπτα, το σύνολο τους μπορεί να περιγραφεί με μαθηματική ακρίβεια.
Νόμος των Μεγάλων Αριθμών:
Ο νόμος των μεγάλων αριθμών δηλώνει ότι καθώς αυξάνεται ο αριθμός των επαναλήψεων ενός τυχαίου πειράματος, ο μέσος όρος των αποτελεσμάτων τείνει να πλησιάσει τη θεωρητική αναμενόμενη τιμή. Αυτό σημαίνει ότι αν ρίξετε ένα νόμισμα πολλές φορές, το ποσοστό των κεφαλών και γραμμάτων θα πλησιάσει το 50%, ακόμη και αν οι πρώτες ρίψεις δώσουν πιο ακραία αποτελέσματα.
Κανονική Κατανομή και Νόμος του Laplace-Gauss:
Η κανονική κατανομή, ή καμπύλη του Gauss, είναι ένα από τα πιο σημαντικά εργαλεία στην πιθανότητα. Περιγράφει πώς κατανέμονται τα δεδομένα γύρω από τη μέση τιμή σε ένα μεγάλο σύνολο παρατηρήσεων και αποτελεί τη βάση για πολλά στατιστικά μοντέλα. Ο νόμος του Laplace-Gauss υποδεικνύει ότι πολλές φυσικές και κοινωνικές μεταβλητές κατανέμονται κανονικά, κάτι που σημαίνει ότι έχουν σχήμα καμπάνας όταν αναπαριστώνται γραφικά.
Αιτιοκρατία και Τυχαίοι Αριθμοί:
Η αιτιοκρατία στη φυσική και τα μαθηματικά αναφέρεται στην ιδέα ότι κάθε γεγονός έχει μια αιτία που το προκαλεί. Ωστόσο, η ύπαρξη τυχαίων αριθμών δείχνει ότι υπάρχουν φαινόμενα που, αν και αιτιοκρατικά, εμφανίζονται ως τυχαία λόγω της πολυπλοκότητας των αιτιών ή της αδυναμίας μας να γνωρίζουμε όλες τις παραμέτρους.