«Τρεις χιλιετίες λογικής» (60 λεπτά)
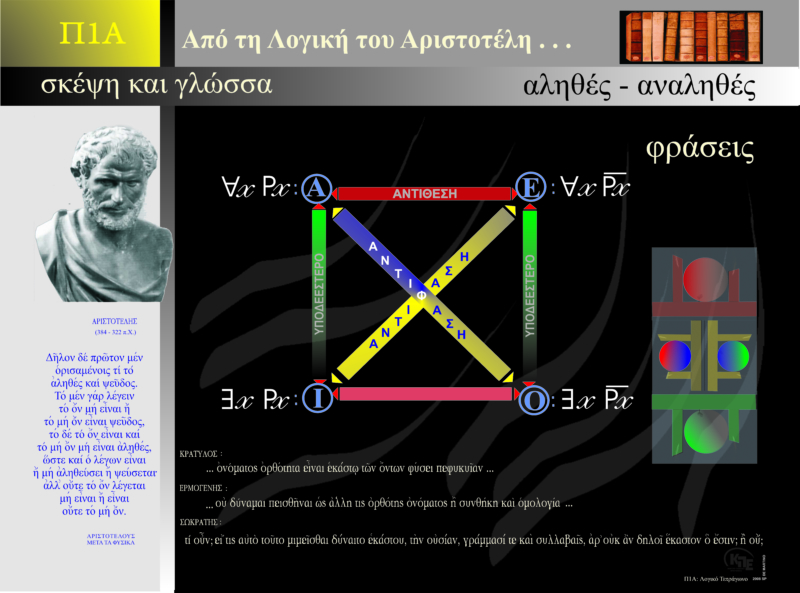
Ο Αριστοτέλης (384-322 π.Χ) ήταν ένας Αρχαίος Έλληνας Φιλόσοφος κι επιστήμονας. Σε ηλικία μόλις 17 ετών εισήλθε στην Ακαδημία του Πλάτωνα στην Αθήνα και παρέμεινε μέχρι τα 37 του χρόνια. Κατά την παραμονή του στην Ακαδημία ήρθε σε επαφή με διάφορους στοχαστές όπως ο Πλάτωνας, ο Εύδοξος καθώς και ο Ξενοκράτης. Μέσα από τα έργα του ασχολήθηκε με πολλούς τομείς όπως η φυσική, η βιολογία, η ποίηση, το θέατρο, η μουσική και άλλες. Σύμφωνα με τον Αριστοτέλη, όλα όσα έχουμε μέσα στο μυαλό μας, ως ιδέες και σκέψεις, έχουν φτάσει μέχρι τη συνείδηση μας χάρη σε όλα όσα έχουμε δει κι ακούσει. Σαν ανθρώπινα όντα έχουμε ένα μυαλό που είναι κατασκευασμένο από τη γέννησή μας να σκέφτεται λογικά. Επίσης οι άνθρωποι έχουν την ικανότητα να τακτοποιούν τις εμπειρίες τους καθώς και όλα όσα αντιλαμβάνονται ως αισθήσεις με λογικό τρόπο σε κατηγορίες και είδη. Για παράδειγμα, στο ανθρώπινο μυαλό υπάρχουν έννοιες όπως «άνθρωποι», «πέτρες», «φυτά» και «ζώα». Η λογική για τον Αριστοτέλη δεν είναι αυτόνομη επιστήμη, είναι όμως χρήσιμη για τον κάθε επιστήμονα καθώς αποτελεί ζωτικής σημασίας εργαλείο γι’ αυτόν. Κατά τον Αριστοτέλη, συλλογισμός είναι μια αλληλουχία σκέψεων που μπαίνει σε λειτουργία όταν τεθεί κάποιο ζήτημα. Με την εμφάνιση του συγκεκριμένου ζητήματος ακολουθεί κάποια σκέψη, η οποία είναι συνέπεια της αλήθειας του ζητήματος. Και αυτό συνεχίζεται χωρίς να χρειάζονται επιπρόσθετα στοιχεία.
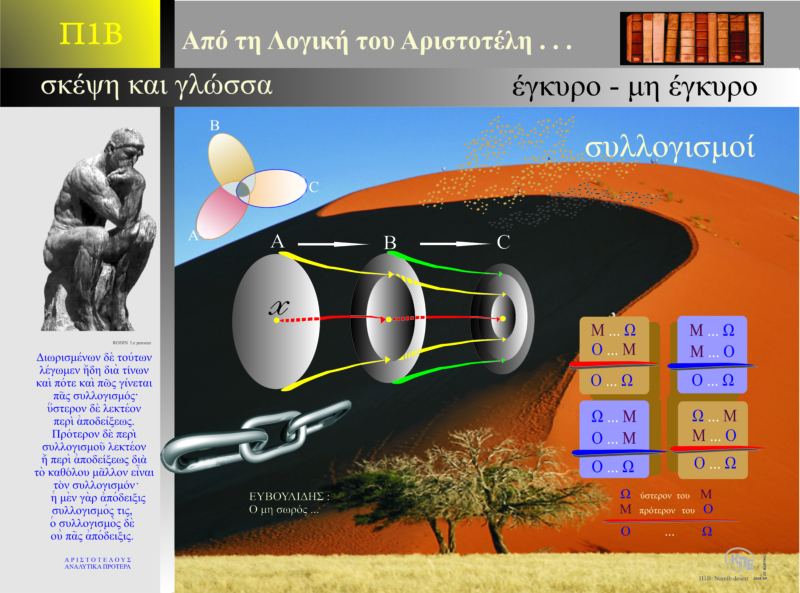
Ο Αριστοτέλης μίλησε για τον συλλογισμό και την επαγωγή. Από τη μια, ο παραγωγικός αποδεικτικός συλλογισμός λειτουργεί ανεξάρτητα από την εμπειρία, έχει απόλυτο κύρος και οδηγεί σε καθολικά συμπεράσματα, ενώ από την άλλη η επαγωγή δεν έχει αποδεικτικό χαρακτήρα, όπως ο συλλογισμός, αφού δε μας διαβεβαιώνει για οποιαδήποτε λογική αναγκαιότητα. Ο συλλογισμός μαζί με την επαγωγή συνιστούν τον τρόπο του ανθρώπου για να γνωρίζει την πραγματικότητα.
Κατά τον Αριστοτέλη, ο συλλογισμός ξεκινά από ορισμένους «λόγους», προτάσεις από τις οποίες μπορεί να παραχθεί μια άλλη πρόταση χωρίς να υπεισέρχεται κάποιος εξωτερικός όρος. Άρα, οι προκείμενες προτάσεις αποτελούν άμεσες αλήθειες, οι οποίες δε χρειάζονται κάποιον εξωτερικό παράγοντα για να συμπληρώσουν το νόημα. Η παραγωγή της συμπερασματικής πρότασης γίνεται με αναγκαίο τρόπο, όταν οι προκείμενες προτάσεις είναι επαρκείς, εμπεριέχουν δηλαδή όλα εκείνα τα στοιχεία που χρειάζονται για να παραχθεί με αναγκαίο τρόπο το συμπέρασμα. Το συμπέρασμα για να είναι αποδεκτό, επιστημονικό και να έχει αποδεικτική λειτουργία προϋποθέτει δύο όρους: α) να είναι γνώση του καθόλου και όχι του καθ’ έκαστον και β) να έχει βεβαιωτικό χαρακτήρα και να αποκλείει την οποιαδήποτε αμφιβολία. Αυτός είναι ο τέλειος συλλογισμός, κατά τον Αριστοτέλη, μια λογική δομή προτάσεων στην οποία τίποτα δε λείπει και τίποτα δεν περισσεύει.
Συμπερασματικά, βάσει του συλλογισμού του Αριστοτέλη: Α→ Β→ Γ
Το έργο «Όργανον» του Αριστοτέλη αποτελεί τη βάση της κλασικής λογικής καθώς και θεμέλιο λίθο για τη δυτική φιλοσοφία αλλά κι επιστήμη. Είναι το έργο που κατέστησε τον Αριστοτέλη «πατέρα της λογικής». Περιλαμβάνει τη διδασκαλία του μεγάλου φιλοσόφου για τη λογική, τον συλλογισμό και την επιχειρηματολογία.
Η ονομασία «Όργανον» δεν αποδόθηκε στα κείμενα αυτά από τον ίδιο τον Αριστοτέλη, αλλά από πολύ μεταγενέστερους μελετητές του, που ήθελαν με την ονομασία αυτή να δείξουν πως η λογική αποτελεί ένα εργαλείο, ένα όργανο για όποιον επιθυμεί να σκεφτεί μεθοδικά.
Tο έργο αυτό πραγματεύεται τις πλέον κεντρικές έννοιες της λογικής όπως:
- η δομή των λογικών προτάσεων και των συλλογισμών,
- η διαφορά μεταξύ επαγωγικής και απαγωγικής σκέψης,
- η φύση της επιστημονικής γνώσης,
- η έννοια της πλάνης ή παραπληροφόρησης καθώς και άλλα.
«Μια υπέροχη παρέα» (60 λεπτά)

Το 1645, ο Γάλλος μαθηματικός Blaise Pascal κατασκεύασε την πρώτη αληθινή αριθμομηχανή, η οποία επονομάστηκε Πασκαλίνα (Pascaline). Με την Pascaline μπορούσαν να εκτελεστούν εύκολοι σχετικά μαθηματικοί υπολογισμοί. Η μηχανή αυτή του Pascal ήταν μικρών διαστάσεων και αποτελούνταν από τροχαλίες οι οποίες όταν περιστρέφονταν από τον χρήστη εμφάνιζαν τα αποτελέσματα. Ο αρχικός «υπολογιστής» είχε πέντε γρανάζια (με αποτέλεσμα να μπορεί να κάνει υπολογισμούς με σχετικά μικρούς αριθμούς), αλλά κατασκευάστηκε και σε παραλλαγές με έξι και οκτώ γρανάζια. Η μηχανή αυτή μπορούσε να εκτελέσει μόνο δύο πράξεις, την πρόσθεση και την αφαίρεση. Στο επάνω μέρος υπήρχε μια σειρά από οδοντωτούς τροχούς τα λεγόμενα γρανάζια, όπου το καθένα περιείχε τους αριθμούς από 0 έως 9. Ο πρώτος τροχός συμβόλιζε τις μονάδες, ο δεύτερος τις δεκάδες, ο τρίτος τις εκατοντάδες, κ.ο.κ.
Το 1673, ο μαθηματικός και φιλόσοφος Gottfried Wilhelm Leibniz (1646-1716) τελειοποίησε τη μηχανή του Pascal φτιάχνοντας μια χειροκίνητη «υπολογιστική μηχανή» ώστε να μπορεί να εκτελεί εκτός από πρόσθεση και αφαίρεση, πολλαπλασιασμούς και διαιρέσεις. Στα αρχικά στάδια της καριέρας του, επινόησε το δυαδικό αριθμητικό σύστημα (0 και 1) που αποτελεί μέχρι και σήμερα τη βάση για τις γλώσσες προγραμματισμού των υπολογιστών. Η μηχανή αυτή βρίσκεται σήμερα σε τεχνικό μουσείο της Γερμανίας.

Ο Άγγλος μαθηματικός, φιλόσοφος και μελετητής της λογικής George Boole (1815 – 1864) με τις δύο του εργασίες: "Μαθηματική Ανάλυση της Λογικής" (1847) και "Έρευνα στους νόμους της σκέψης στους οποίους στηρίζονται οι μαθηματικές θεωρίες της λογικής και οι πιθανότητες" (1854) μετέτρεψε την προτασιακή λογική σε μια άλγεβρα του συνόλου Β = εφοδιασμένη με τις πράξεις «+» και «•».
Η Αριστοτέλεια λογική βάσει της οποίας «είναι αδύνατον η ίδια ιδιότητα να ανήκει και να μην ανήκει στο ίδιο αντικείμενο» (αρχή της αντίφασης) μεταφράζεται βάσει της Άλγεβρας Boole ως «τίποτα δεν μπορεί να ανήκει και συγχρόνως να μην ανήκει σε μια δεδομένη κλάση».
Το δημιούργημα του Boole στηρίχθηκε πάνω στις αρχές της ευρύτερης άλγεβρας, έχοντας όμως μια πολύ συγκεκριμένη δομή. Σε αντίθεση με την στοιχειώδη άλγεβρα, όπου οι τιμές των μεταβλητών είναι αριθμοί και οι κύριες πράξεις είναι η πρόσθεση και ο πολλαπλασιασμός, η άλγεβρα Boole εμφανίζει μόνο τις τιμές «1» και «0». Παράλληλα έχει τρεις κύριες πράξεις, τη σύζευξη «Λ», τη διάζευξη «V» και την άρνηση «-».

Ο Friedrich Ludwig Gottlob Frege (1848-1925) υπήρξε Γερμανός μαθηματικός, λογικολόγος και φιλόσοφος ο οποίος θεμελίωσε τις σύγχρονες γλώσσες προγραμματισμού.
Οι εργασίες του στη Λογική, στη Φιλοσοφία των Μαθηματικών, στη Φιλοσοφική Λογική και στη θεωρία νοήματος αποτελούν αφετηρία και σημεία αναφοράς για τις μετέπειτα έρευνες για τους τομείς αυτούς. Ο Frege εισήγαγε ένα σύστημα συμβολικής Λογικής που επεκτείνει κατά πολύ την Αριστοτελική Λογική, ενώ παράλληλα επιχείρησε την αναγωγή της Αριθμητικής στη Λογική έτσι ώστε να καταδείξει ότι οι προτάσεις της Αριθμητικής είναι αναλυτικές και εισήγαγε τις κεντρικές για τη θεωρία του νοήματος έννοιες της σημασίας και της αναφοράς.
Οι εργασίες του Frege στη θεωρία νοήματος, έχουν αφετηρία την αναζήτηση ενός συστήματος εννοιολογικού συμβολισμού της καθαρής σκέψης, στο οποίο θα μπορούμε να ελέγχουμε με τον πλέον αξιόπιστο τρόπο την εγκυρότητα κάθε συλλογισμού και να αποκαλύπτουμε όλες τις προϋποθέσεις που υπεισέρχονται, συχνά με λανθάνοντα τρόπο, στους συλλογισμούς.
Αυτό το σύστημα συμβολισμού θα αποτελούσε, κατά κάποιο τρόπο, την πραγμάτωση του ιδεώδους του Leibniz για μια καθολική γλώσσα. Σε ένα τέτοιο πλαίσιο αναζήτησης, ο Frege οδηγείται στη διάκριση ανάμεσα στη σημασία και την αναφορά μιας γλωσσικής έκφρασης και αποστασιοποιεί το νόημα των γλωσσικών εκφράσεων από την υποκειμενική ιδέα, παράσταση και εν γένει τα ψυχολογικά συμβάντα.
Η θεωρία νοήματος του Frege βασίζεται στη διάκριση ανάμεσα στη σημασία και την αναφορά μιας γλωσσικής έκφρασης και εισάγεται έπειτα από την απόρριψη μιας απλοϊκής αναπαραστασιακής θεώρησης του νοήματος και έπειτα από την απόρριψη του ψυχολογισμού, της θέσης ότι το νόημα είναι μια ψυχολογική οντότητα και οι λογικές σχέσεις είναι ψυχολογικές διασυνδέσεις. Σύμφωνα με τον Frege, το νόημα μιας γλωσσικής έκφρασης δεν συνίσταται σε έναν απλό συσχετισμό ανάμεσα στην έκφραση και κάποιο αντικείμενο αλλά ούτε και σε μια ιδέα ή νοητική παράσταση.
«Δύο αριθμοί είναι υπέρ-αρκετοί» (60 λεπτά)

Το πέρασμα στην Τεχνολογία – Από το νοητό στο αισθητό – Δομές δεδομένων οργάνωση
Στη σύγχρονη τεχνολογία των υπολογιστών, η οργάνωση των δεδομένων είναι θεμελιώδης για την αποδοτική λειτουργία των συστημάτων. Το πέρασμα από το νοητό – τις αφηρημένες έννοιες της λογικής και των μαθηματικών – στο αισθητό – τη φυσική εφαρμογή αυτών των εννοιών σε πραγματικές συσκευές – έγινε εφικτό μέσω της ανάπτυξης των δομών δεδομένων. Οι δομές δεδομένων επιτρέπουν στους υπολογιστές να αποθηκεύουν, να επεξεργάζονται και να ανακτούν τεράστιες ποσότητες πληροφοριών με ακρίβεια και ταχύτητα.
Δομές δεδομένων: Οργάνωση και αποδοτικότητα
Οι δομές δεδομένων είναι συγκεκριμένοι τρόποι οργάνωσης και αποθήκευσης πληροφοριών στη μνήμη του υπολογιστή, έτσι ώστε τα δεδομένα να μπορούν να χρησιμοποιηθούν αποτελεσματικά. Κάθε δομή δεδομένων είναι σχεδιασμένη για να εξυπηρετεί διαφορετικούς τύπους εφαρμογών και να επιτρέπει γρήγορη πρόσβαση και διαχείριση των δεδομένων.
– Πίνακες (Arrays): Πρόκειται για μια από τις πιο βασικές δομές δεδομένων, όπου τα δεδομένα αποθηκεύονται σε μια σειρά διαδοχικών θέσεων μνήμης. Οι πίνακες παρέχουν γρήγορη πρόσβαση σε συγκεκριμένα στοιχεία, αλλά είναι στατικοί και δεν μπορούν εύκολα να αλλάξουν μέγεθος.
– Συνδεδεμένες λίστες (Linked Lists): Αυτή η δομή επιτρέπει την αποθήκευση δεδομένων σε μη συνεχόμενες θέσεις μνήμης, χρησιμοποιώντας συνδέσμους για να συνδέει τα δεδομένα μεταξύ τους. Οι λίστες προσφέρουν ευελιξία σε ό,τι αφορά την προσθήκη και αφαίρεση στοιχείων, αλλά μπορεί να είναι αργές σε λειτουργίες όπως η αναζήτηση.
– Δέντρα (Trees): Τα δέντρα είναι ιεραρχικές δομές δεδομένων, όπου τα δεδομένα οργανώνονται σε “κόμβους” με γονείς και παιδιά. Τα δέντρα χρησιμοποιούνται ευρέως για την αποθήκευση δεδομένων με ιεραρχικές σχέσεις, όπως αρχεία σε ένα σύστημα φακέλων.
– Γραφήματα (Graphs): Τα γραφικά μοντέλα χρησιμοποιούνται για την αναπαράσταση περίπλοκων σχέσεων μεταξύ των δεδομένων. Σε ένα γράφημα, τα δεδομένα αναπαρίστανται ως κόμβοι και οι συνδέσεις τους ως ακμές.
Η συνεισφορά του John von Neumann
Ο John von Neumann ήταν ένας από τους θεμελιωτές της σύγχρονης πληροφορικής και είναι γνωστός για την αρχιτεκτονική που φέρει το όνομά του. Η **αρχιτεκτονική von Neumann** εισήγαγε την ιδέα ότι ένας υπολογιστής θα πρέπει να αποθηκεύει τόσο τα δεδομένα όσο και τις εντολές στη μνήμη του. Αυτή η αρχή απλοποίησε τη σχεδίαση των υπολογιστικών συστημάτων και αποτελεί τη βάση για όλους τους σύγχρονους υπολογιστές.
Με αυτή την αρχιτεκτονική, ο υπολογιστής μπορούσε να αποθηκεύει μεγάλα ποσά πληροφοριών στη μνήμη του και να εκτελεί προγράμματα πιο αποδοτικά, χωρίς να χρειάζεται εξωτερική εισαγωγή κάθε φορά. Η δομή δεδομένων και η αποθήκευση ήταν καίρια για την ανάπτυξη των σύγχρονων υπολογιστών, επιτρέποντας τη συνεχή εκτέλεση πολλαπλών προγραμμάτων και τη διαχείριση σύνθετων διαδικασιών.
Οργάνωση και διαχείριση δεδομένων: Θεμέλιο της τεχνολογίας
Οι δομές δεδομένων διαδραματίζουν κρίσιμο ρόλο στην αποτελεσματική διαχείριση των πληροφοριών. Η επιλογή της κατάλληλης δομής για την οργάνωση των δεδομένων εξαρτάται από τη φύση της εφαρμογής και τις απαιτήσεις απόδοσης. Ένα καλά οργανωμένο σύστημα δεδομένων μπορεί να βελτιώσει δραματικά την απόδοση των υπολογιστών, επιταχύνοντας τις διαδικασίες ανάκτησης, επεξεργασίας και αποθήκευσης πληροφοριών.
Επίσης, οι δομές δεδομένων επιτρέπουν στους υπολογιστές να διαχειρίζονται μεγάλα σύνολα δεδομένων με πιο αποδοτικό τρόπο, είτε πρόκειται για βάσεις δεδομένων, εφαρμογές τεχνητής νοημοσύνης ή για οποιοδήποτε άλλο σύστημα που απαιτεί γρήγορη πρόσβαση και επεξεργασία πληροφοριών.
Συμπέρασμα
Tο πέρασμα από το νοητό στο αισθητό στην τεχνολογία, ειδικά στο πλαίσιο των δομών δεδομένων, αποτελεί ένα από τα πιο σημαντικά επιτεύγματα της σύγχρονης πληροφορικής. Οι δομές δεδομένων είναι ζωτικής σημασίας για την αποθήκευση και οργάνωση πληροφοριών με αποδοτικό τρόπο, ενώ οι ιδέες του John von Neumann για την αρχιτεκτονική των υπολογιστών συνέβαλαν καθοριστικά στην ανάπτυξη των σημερινών συστημάτων. Χάρη σε αυτές τις καινοτομίες, οι υπολογιστές μπορούν να επεξεργάζονται τεράστιες ποσότητες δεδομένων με ακρίβεια και ταχύτητα, κάνοντας δυνατή τη δημιουργία της ψηφιακής εποχής στην οποία ζούμε σήμερα.
«Είσαι πιο έξυπνος από έναν υπολογιστή;» (80 λεπτά)

Η σημασία των αλγορίθμων και η συμβολή του Μουχάμαντ αλ-Χουαρίζμι (Al-Khwarizmi) στην ανάπτυξη της μαθηματικής επιστήμης και του προγραμματισμού αποτελεί βασικό σημείο κατανόησης της εξέλιξης των επιστημών. Η λεπτομερής ανασκόπηση της δουλειάς του και ο τρόπος με τον οποίο επηρέασε τη σύγχρονη σκέψη για την επίλυση προβλημάτων μέσω αλγοριθμικών διαδικασιών αποκαλύπτουν τη βαθιά σχέση ανάμεσα στα μαθηματικά, την επιστήμη των υπολογιστών και την τεχνητή νοημοσύνη.
- Η Ιστορική Κληρονομιά του Al-Khwarizmi
Ο Μουχάμαντ αλ-Χουαρίζμι, που έζησε μεταξύ του 780 και του 850 μ.Χ., ήταν από τους πρώτους μαθηματικούς και αστρονόμους της εποχής του. Εργάστηκε στο **Οίκο της Σοφίας** (Bayt al-Hikma) στη Βαγδάτη, μια βιβλιοθήκη και ακαδημαϊκό κέντρο που υποστήριζε την επιστημονική μελέτη και την προώθηση των μαθηματικών, της γεωμετρίας, της αστρονομίας και της λογιστικής. Εκεί, μεταφράστηκαν πολλά έργα των αρχαίων Ελλήνων και Ινδών μαθηματικών, που είχαν σημαντική επιρροή στη σκέψη του Al-Khwarizmi.
Το σημαντικότερο έργο του Al-Khwarizm* ήταν το βιβλίο του Al-Kitab al-Mukhtasar fi Hisab al-Jabr wal-Muqabala (“Η σύντομη βιβλίο για τον υπολογισμό με ολοκλήρωση και εξίσωση”). Στο έργο αυτό εισάγει τον αναλυτικό τρόπο επίλυσης εξισώσεων μέσω κανόνων που σήμερα ονομάζουμε αλγεβρικούς κανόνες. Ο όρος “άλγεβρα” (al-jabr) προέρχεται από το βιβλίο αυτό, συγκεκριμένα από την αραβική λέξη “jabr”, που αναφέρεται στη διαδικασία της αναδόμησης και της μετατροπής εξισώσεων.
Αλλά το πιο εντυπωσιακό κομμάτι της κληρονομιάς του Al-Khwarizmi είναι η ανάπτυξη της έννοιας του αλγορίθμου. Ο όρος “αλγόριθμος” προέρχεται από το όνομά του και χρησιμοποιείται για να περιγράψει μια ακριβή, επαναλαμβανόμενη διαδικασία που μπορεί να εφαρμοστεί για να λυθούν συγκεκριμένα προβλήματα. Το έργο του στον τομέα των αριθμητικών μεθόδων περιελάμβανε και τη χρήση των Ινδικών αριθμών (που αργότερα ονομάστηκαν αραβικοί αριθμοί), και οι μέθοδοί του ήταν ένας πρώιμος τρόπος εισαγωγής των αριθμών στο σύστημα αρίθμησης με βάση το δέκα.
- Τι Είναι οι Αλγόριθμοι;
Οι αλγόριθμοι αποτελούν βασικό στοιχείο στην επίλυση προβλημάτων, όχι μόνο στον τομέα των μαθηματικών αλλά και σε πολλές άλλες επιστήμες και τομείς της ζωής. Ένας αλγόριθμος είναι μια προκαθορισμένη σειρά βημάτων ή εντολών που εφαρμόζονται για να λυθεί ένα πρόβλημα ή να επιτευχθεί ένα συγκεκριμένο αποτέλεσμα. Οι αλγόριθμοι δεν αφορούν μόνο τις αριθμητικές πράξεις· χρησιμοποιούνται σε σχεδόν κάθε διαδικασία από τη λογική μέχρι τη μηχανική και την τεχνητή νοημοσύνη.
Για παράδειγμα, σκεφτείτε την ταξινόμηση (sorting) ενός συνόλου δεδομένων. Ένας αλγόριθμος ταξινόμησης μπορεί να εφαρμοστεί για να ανακατατάξει στοιχεία, όπως αριθμούς ή ονόματα, σε αύξουσα ή φθίνουσα σειρά. Ένας από τους πιο απλούς αλγορίθμους είναι ο αλγόριθμος φυσαλίδων (bubble sort), ο οποίος συγκρίνει διαδοχικά τα στοιχεία και τα αλλάζει εφόσον δεν βρίσκονται στη σωστή σειρά. Αυτή η απλή διαδικασία είναι μια βασική μορφή αλγορίθμου.
Η έννοια του αλγορίθμου, όπως την εισήγαγε ο Al-Khwarizmi, επικεντρώνεται στη λογική ανάλυση και τη διάσπαση σύνθετων προβλημάτων σε απλούστερα βήματα. Αυτή η μεθοδολογία αποτελεί το θεμέλιο της σύγχρονης υπολογιστικής σκέψης, όπου τα προβλήματα αναλύονται σε μικρότερες, πιο διαχειρίσιμες ενότητες.
- Αλγόριθμοι και Ταξινόμηση
Η ταξινόμηση (sorting) είναι ένα από τα πρώτα και πιο σημαντικά προβλήματα που αντιμετωπίζονται στην επιστήμη των υπολογιστών. Ο σκοπός της ταξινόμησης είναι η αναδιάταξη ενός συνόλου δεδομένων με βάση κάποιο συγκεκριμένο κριτήριο, π.χ. αριθμητικά ή αλφαβητικά. Οι αλγόριθμοι ταξινόμησης είναι κρίσιμοι για πολλές εφαρμογές, από την αναζήτηση δεδομένων μέχρι την ανάλυση μεγάλων συνόλων δεδομένων.
Μερικοί από τους πιο γνωστούς αλγορίθμους ταξινόμησης περιλαμβάνουν:
– Αλγόριθμος Φυσαλίδων (Bubble Sort): Σταδιακά συγκρίνει και αλλάζει στοιχεία που είναι σε λάθος σειρά. Αν και είναι απλός, είναι αργός για μεγάλες λίστες δεδομένων.
– Ταξινόμηση Με Επιλογή (Selection Sort): Βρίσκει το μικρότερο στοιχείο από μια λίστα και το τοποθετεί στη σωστή θέση, επαναλαμβάνοντας τη διαδικασία για όλα τα στοιχεία.
– Γρήγορη Ταξινόμηση (Quick Sort): Χωρίζει ένα σύνολο δεδομένων σε μικρότερα μέρη και εφαρμόζει αναδρομικά τη διαδικασία ταξινόμησης. Είναι ένας από τους πιο γρήγορους και αποτελεσματικούς αλγορίθμους ταξινόμησης.
Αυτοί οι αλγόριθμοι χρησιμοποιούν ακριβώς την αρχή της διάσπασης των προβλημάτων σε βήματα, όπως διδάχθηκε από τον Al-Khwarizmi. Κατά κάποιο τρόπο, η επίλυση του προβλήματος της ταξινόμησης αντικατοπτρίζει τη λογική και τη μαθηματική προσέγγιση που εισήγαγε ο Al-Khwarizmi στον μεσαιωνικό κόσμο.
- Οι Αλγόριθμοι στη Σύγχρονη Εποχή: Τεχνητή Νοημοσύνη και Μηχανική Μάθηση
Στη σημερινή εποχή, οι αλγόριθμοι έχουν επεκταθεί από τη μαθηματική θεωρία και τον προγραμματισμό σε νέες τεχνολογίες, όπως η τεχνητή νοημοσύνη (AI) και η μηχανική μάθηση (ML). Η τεχνητή νοημοσύνη βασίζεται στην ικανότητα των αλγορίθμων να μαθαίνουν και να βελτιώνονται με την πάροδο του χρόνου, αναλύοντας δεδομένα και αναγνωρίζοντας πρότυπα. Η μηχανική μάθηση βασίζεται στη χρήση αλγορίθμων που επιτρέπουν στους υπολογιστές να μαθαίνουν χωρίς να είναι ρητά προγραμματισμένοι.
Ένα παράδειγμα τέτοιων αλγορίθμων είναι οι αλγόριθμοι νευρωνικών δικτύων, οι οποίοι μιμούνται τον τρόπο που ο εγκέφαλος αναλύει και επεξεργάζεται πληροφορίες. Αυτά τα συστήματα χρησιμοποιούν αλγοριθμικές διαδικασίες για να αναλύσουν τεράστια δεδομένα και να δημιουργήσουν προγνώσεις ή αποφάσεις βάσει αυτών των δεδομένων.
Η συμβολή του Al-Khwarizmi στην ανάπτυξη της αλγοριθμικής σκέψης είναι εμφανής ακόμη και σε αυτές τις σύγχρονες εφαρμογές. Ο τρόπος με τον οποίο αναλύουμε προβλήματα, προγραμματίζουμε συστήματα και αναζητούμε λύσεις σε πολύπλοκα θέματα βασίζεται στις θεμελιώδεις αρχές που εκείνος έθεσε πριν από περισσότερους από 1.000 χρόνια.
Συμπέρασμα
Η κληρονομιά του Al-Khwarizmi είναι αναμφισβήτητα μια από τις πιο σημαντικές στην ιστορία των μαθηματικών και της επιστήμης των υπολογιστών. Από την ανάπτυξη της άλγεβρας μέχρι την εισαγωγή των πρώτων αλγορίθμων, το έργο του διαμόρφωσε τον τρόπο με τον οποίο κατανοούμε και επιλύουμε προβλήματα. Σήμερα, οι αλγόριθμοι εξακολουθούν να βρίσκονται στο επίκεντρο της επιστήμης και της τεχνολογίας, επιτρέποντάς μας να δημιουργήσουμε πιο έξυπνες μηχανές, να αναλύσουμε τεράστια δεδομένα και να διαχειριστούμε την πολυπλοκότητα του σύγχρονου κόσμου.
Το πρόβλημα των γεφυρών του Königsberg και η λύση του από τον μαθηματικό Leonhard Euler το 1736 αποτελεί ένα από τα πιο σημαντικά γεγονότα στην ιστορία των μαθηματικών. Η πόλη Königsberg, η οποία βρίσκεται στις όχθες του ποταμού Πρεγκέλ, είχε τότε μια ιδιαίτερη γεωγραφία. Ο ποταμός διαιρούσε την πόλη σε δύο κύριες περιοχές ξηράς και δύο νησιά, τα οποία συνδέονταν με επτά γέφυρες. Ένα γνωστό πρόβλημα της εποχής ήταν αν μπορούσε κάποιος να σχεδιάσει έναν περίπατο που θα διέσχιζε όλες τις γέφυρες ακριβώς μία φορά, χωρίς να περάσει από την ίδια γέφυρα δύο φορές.
Η πρόκληση αυτή φαίνεται απλή, αλλά η πολυπλοκότητά της έκανε πολλούς να αναρωτιούνται αν ήταν πραγματικά εφικτό να επιτευχθεί αυτό το μονοπάτι. Όλοι προσπαθούσαν να βρουν λύση μέσω δοκιμών, αλλά κανείς δεν κατάφερε να το πετύχει. Ωστόσο, ήταν ο Euler που κατάλαβε ότι το πρόβλημα δεν είχε να κάνει μόνο με τη γεωγραφική τοποθέτηση των γεφυρών, αλλά με την αφαιρετική δομή που αυτές σχημάτιζαν.
Η προσέγγιση του Euler
Ο Euler αποφάσισε να αναπαραστήσει την πόλη και τις γέφυρες με έναν πιο αφαιρετικό τρόπο, κάτι που θα έδινε μια καθαρή εικόνα του προβλήματος. Αντί να σκεφτεί τις γέφυρες και τα νησιά όπως είναι στη γεωγραφία, τα αναπαρήγαγε με γραφήματα: κάθε νησί ή περιοχή της ξηράς αντιπροσωπεύτηκε ως μια κορυφή (vertex) και κάθε γέφυρα ως μια ακμή (edge) που συνδέει δύο κορυφές.
Με αυτό τον τρόπο, η πόλη Königsberg αναπαρίστατο από ένα γράφημα με τέσσερις κορυφές, καθεμιά από τις οποίες συνδέεται με ακμές (γέφυρες) με τις υπόλοιπες. Το πρόβλημα του να περπατήσει κάποιος πάνω από κάθε γέφυρα ακριβώς μία φορά μετατράπηκε στο εξής ερώτημα: μπορείς να σχεδιάσεις μια διαδρομή στο γράφημα που θα περάσει από κάθε ακμή ακριβώς μία φορά;
Η ανακάλυψη της αναγκαιότητας της ισότητας
Ο Euler κατέληξε σε μια κρίσιμη παρατήρηση: σε κάθε κορυφή (ή περιοχή) πρέπει ο αριθμός των ακμών που φεύγουν από αυτή να είναι ζυγός, προκειμένου να μπορείς να μπεις και να βγεις από αυτή χωρίς να επιστρέψεις. Για να κατανοήσει κανείς γιατί συμβαίνει αυτό, αρκεί να σκεφτεί ότι αν περάσεις από μια κορυφή, πρέπει να έχεις ένα μονοπάτι για να βγεις πάλι από αυτή. Συνεπώς, αν υπάρχει περιττός αριθμός ακμών που φεύγουν από μια κορυφή, τότε δεν μπορείς να περάσεις από εκεί χωρίς να χρησιμοποιήσεις μία ακμή δεύτερη φορά.
Το πρόβλημα με το γράφημα των γεφυρών του Königsberg ήταν ότι όλες οι κορυφές είχαν περιττό αριθμό ακμών. Αυτό σήμαινε ότι δεν υπήρχε τρόπος να περάσει κάποιος από κάθε γέφυρα ακριβώς μία φορά, χωρίς να επαναλάβει μια γέφυρα.
Το αποτέλεσμα του Euler και η γέννηση της θεωρίας των γραφημάτων
Το τελικό συμπέρασμα του Euler ήταν ότι δεν υπάρχει λύση στο πρόβλημα των γεφυρών του Königsberg. Όμως, αυτή η φαινομενικά απλή διαπίστωση είχε τεράστια μαθηματική σημασία. Ο Euler έβαλε τα θεμέλια για τη θεωρία των γραφημάτων, μια μαθηματική δομή που αναπαριστά ένα σύνολο αντικειμένων που συνδέονται μεταξύ τους. Η θεωρία αυτή χρησιμοποιείται σήμερα σε πολλά διαφορετικά πεδία, από τα δίκτυα υπολογιστών και την κοινωνική δικτύωση, μέχρι τη βιολογία και την τοπολογία.
Επιπλέον, το πρόβλημα των γεφυρών του Königsberg είναι το πρώτο παράδειγμα ενός Eulerian κύκλου ή μονοπατιού. Ένα γράφημα που έχει έναν τέτοιο κύκλο πρέπει να πληροί ορισμένες προϋποθέσεις: όλες οι κορυφές πρέπει να έχουν ζυγό αριθμό ακμών. Αν μόνο δύο κορυφές έχουν περιττό αριθμό ακμών, τότε μπορεί να υπάρξει μονοπάτι που ξεκινά από μία κορυφή και τελειώνει σε μία άλλη, χωρίς να επαναλάβει κάποια ακμή.
Σημαντικότητα του προβλήματος
Η λύση του προβλήματος των γεφυρών του Königsberg αποτελεί ένα ορόσημο στην ιστορία των μαθηματικών και της λογικής. Η σκέψη του Euler να αναπαραστήσει το πρόβλημα με γραφήματα ήταν μια πρωτοποριακή ιδέα που άνοιξε τον δρόμο για μια νέα κατηγορία μαθηματικών προβλημάτων. Σήμερα, η θεωρία των γραφημάτων είναι ένα σημαντικό εργαλείο με πολλές εφαρμογές στην επιστήμη και την τεχνολογία. Από τη χαρτογράφηση των δρόμων μιας πόλης μέχρι την ανάλυση κοινωνικών δικτύων και την κατανόηση μορίων στη χημεία, η θεμελιώδης αρχή που έθεσε ο Euler παραμένει εξαιρετικά χρήσιμη.

«Πύργος του Ανόι» Ο “Πύργος του Ανόι” (γνωστός και ως Tower of Hanoi στα αγγλικά) είναι ένα κλασικό μαθηματικό παιχνίδι λογικής και παζλ, που επινοήθηκε από τον Γάλλο μαθηματικό Édouard Lucas το 1883. Το παιχνίδι έχει να κάνει με τη μετακίνηση δίσκων από έναν πύργο σε έναν άλλο, ακολουθώντας συγκεκριμένους κανόνες.


Οι αλγόριθμοι και η πολυπλοκότητα αποτελούν κεντρικές έννοιες στη σύγχρονη επιστήμη, με εφαρμογές που επεκτείνονται από τα μαθηματικά και την πληροφορική έως τη βιολογία και τη φυσική. Για να κατανοήσουμε καλύτερα πώς οι απλές διαδικασίες μπορούν να οδηγήσουν σε εξαιρετικά πολύπλοκες και οργανωμένες συμπεριφορές, η μελέτη των αλγορίθμων έχει αναδειχθεί ως ένα από τα πιο ισχυρά εργαλεία. Ένα από τα πιο ενδεικτικά παραδείγματα αυτής της αλληλεπίδρασης είναι το “Παιχνίδι της Ζωής” του John Conway, ένα είδος κυψελοειδούς αυτόματου (cellular automaton) που προσομοιώνει την εξέλιξη ενός συστήματος βασισμένου σε απλούς κανόνες.
Τι είναι ένας αλγόριθμος;
Ο αλγόριθμος είναι μια σειρά καλά καθορισμένων κανόνων ή βημάτων που εφαρμόζονται για την επίλυση ενός προβλήματος ή την εκτέλεση μιας διαδικασίας. Στη ρίζα του, οι αλγόριθμοι είναι απλοί, ωστόσο η εφαρμογή τους μπορεί να οδηγήσει σε πολύπλοκα και μη προβλέψιμα αποτελέσματα. Αυτός ο χαρακτηρισμός της «πολυπλοκότητας» αφορά συχνά την αλληλεπίδραση πολλών απλών στοιχείων ή παραγόντων μέσα σε ένα σύστημα, τα οποία δημιουργούν συλλογικά πλούσιες και πολύπλοκες δομές.
Το “Παιχνίδι της Ζωής” του Conway: Ένα παράδειγμα πολυπλοκότητας
Το “Παιχνίδι της Ζωής” είναι ένα παράδειγμα που δείχνει πώς οι αλγόριθμοι μπορούν να γεννήσουν πολυπλοκότητα μέσα από απλούς κανόνες. Το παιχνίδι αυτό είναι ένα κυψελοειδές αυτόματο όπου ένα πλέγμα κυττάρων μπορεί να βρίσκεται σε δύο καταστάσεις: “ζωντανό” ή “νεκρό”. Οι κανόνες που ορίζουν την εξέλιξη του συστήματος είναι εξαιρετικά απλοί:
- Ένα ζωντανό κύτταρο πεθαίνει εάν έχει λιγότερους από δύο ή περισσότερους από τρεις ζωντανούς γείτονες (υπερπληθυσμός ή μοναξιά).
- Ένα ζωντανό κύτταρο επιβιώνει εάν έχει δύο ή τρεις ζωντανούς γείτονες.
- Ένα νεκρό κύτταρο ξαναγεννιέται εάν έχει ακριβώς τρεις ζωντανούς γείτονες.
Αυτοί οι τρεις κανόνες είναι η βάση για τη δημιουργία εκπληκτικής ποικιλίας προτύπων και δομών, ορισμένα από τα οποία παραμένουν σταθερά, άλλα αναπαράγονται ή κινούνται στο χώρο, ενώ ορισμένα εξαφανίζονται. Αυτό που κάνει το “Παιχνίδι της Ζωής” τόσο ενδιαφέρον είναι ότι από την απλότητα των κανόνων του προκύπτει εξαιρετικά πλούσια συμπεριφορά, μια ένδειξη της φύσης των πολύπλοκων συστημάτων.
Πολυπλοκότητα και Φυσικά Συστήματα
Η ιδέα ότι απλοί κανόνες μπορούν να οδηγήσουν σε πολυπλοκότητα δεν είναι αποκλειστική για την πληροφορική ή τα μαθηματικά. Στη φύση, πολλές διαδικασίες που φαίνονται περίπλοκες μπορούν να εξηγηθούν από απλούς κανόνες αλληλεπίδρασης. Για παράδειγμα, η εξέλιξη των ειδών μέσω φυσικής επιλογής, όπως περιγράφεται από τον Δαρβίνο, βασίζεται σε έναν απλό αλγόριθμο: τα ζώα με τα καλύτερα χαρακτηριστικά επιβιώνουν και αναπαράγονται. Ωστόσο, μέσα από εκατομμύρια χρόνια αλληλεπιδράσεων και μεταλλάξεων, αυτός ο κανόνας έχει οδηγήσει σε έναν τεράστιο πλούτο ζωής με αμέτρητα διαφορετικά είδη.
Παρομοίως, η ανάπτυξη ενός εμβρύου από ένα απλό κύτταρο σε έναν πλήρως λειτουργικό οργανισμό βασίζεται σε γενετικούς αλγόριθμους. Τα γονίδια, που περιέχουν τις πληροφορίες για τη δημιουργία και τη λειτουργία ενός οργανισμού, καθορίζουν μια σειρά απλών οδηγιών, οι οποίες αλληλεπιδρούν με το περιβάλλον και τα άλλα κύτταρα για να οδηγήσουν σε εξαιρετικά πολύπλοκες δομές, όπως το ανθρώπινο σώμα.
Η Αναζήτηση Αλγορίθμων στην Επιστήμη
Η αναζήτηση αλγορίθμων είναι μια από τις βασικές προσπάθειες στην επιστήμη, καθώς οι ερευνητές προσπαθούν να κατανοήσουν πώς λειτουργούν τα συστήματα και πώς μπορούν να προσομοιωθούν ή να αναπαραχθούν. Στην πληροφορική, οι αλγόριθμοι χρησιμοποιούνται για την επεξεργασία τεράστιων ποσοτήτων δεδομένων, για την ανάπτυξη τεχνητής νοημοσύνης και για τη μοντελοποίηση φυσικών φαινομένων. Η ανάπτυξη νέων αλγορίθμων επιτρέπει στους επιστήμονες να κατανοούν καλύτερα τη δομή των δεδομένων, να αναγνωρίζουν προτύπα και να προβλέπουν μελλοντικές συμπεριφορές.
Ένας άλλος τομέας όπου η αναζήτηση αλγορίθμων είναι ζωτικής σημασίας είναι η μοντελοποίηση της ζωής και της εξέλιξης. Οι αλγόριθμοι που χρησιμοποιούνται σε προσομοιώσεις της βιολογίας και της εξέλιξης μπορούν να βοηθήσουν στην κατανόηση των μηχανισμών που διέπουν τη ζωή και την πολυπλοκότητα. Για παράδειγμα, οι γενετικοί αλγόριθμοι, που μιμούνται τη διαδικασία της φυσικής επιλογής, χρησιμοποιούνται ευρέως στην επιστήμη των υπολογιστών για τη βελτιστοποίηση και την επίλυση προβλημάτων.
Η Πολυπλοκότητα στη Ζωή και στη Μηχανική Μάθηση
Σήμερα, με την άνοδο της τεχνητής νοημοσύνης και της μηχανικής μάθησης, οι αλγόριθμοι παίζουν καθοριστικό ρόλο στην κατανόηση της πολυπλοκότητας. Η μηχανική μάθηση βασίζεται σε αλγόριθμους που επιτρέπουν στα μηχανήματα να “μαθαίνουν” από τα δεδομένα και να αναπτύσσουν μοτίβα ή συμπεριφορές που προκύπτουν από σύνθετες αλληλεπιδράσεις. Εδώ, η πολυπλοκότητα δεν είναι μόνο ένα φυσικό φαινόμενο, αλλά κάτι που μπορεί να δημιουργηθεί από αλγοριθμικές διαδικασίες, δίνοντάς μας νέα εργαλεία για την επίλυση προβλημάτων που προηγουμένως θεωρούνταν άλυτα.
Συμπέρασμα
Οι αλγόριθμοι και η πολυπλοκότητα είναι θεμελιώδη στοιχεία για την κατανόηση του κόσμου γύρω μας. Από τα απλά κυψελοειδή αυτόματα όπως το “Παιχνίδι της Ζωής” έως τα εξαιρετικά περίπλοκα φυσικά συστήματα, οι αλγόριθμοι μας επιτρέπουν να δούμε πώς η αλληλεπίδραση απλών κανόνων μπορεί να δημιουργήσει την πολυπλοκότητα της φύσης. Η αναζήτηση νέων αλγορίθμων συνεχίζεται, καθώς η κατανόηση της πολυπλοκότητας είναι το κλειδί για να ξεκλειδώσουμε τα μυστικά της ζωής, της εξέλιξης και της ίδιας της ύπαρξης.

Οι αλγόριθμοι αποτελούν τα θεμελιώδη εργαλεία για την επίλυση προβλημάτων που εμπλέκουν πολυπλοκότητα, και ο λαβύρινθος είναι μια εξαιρετική αναλογία που δείχνει πώς οι αλγόριθμοι μπορούν να εφαρμοστούν στην πράξη. Ο λαβύρινθος απεικονίζει ένα πολύπλοκο σύστημα επιλογών και διαδρομών, που αντιπροσωπεύει την ανάγκη για εξερεύνηση και δοκιμή διαφορετικών στρατηγικών για να βρεθεί η βέλτιστη λύση.
Ας εξετάσουμε πιο λεπτομερώς τα βασικά στοιχεία που κάνουν έναν αλγόριθμο τόσο σημαντικό για την επίλυση τέτοιων προβλημάτων.
- Τι είναι η πολυπλοκότητα;
Η πολυπλοκότητα σε ένα πρόβλημα αναφέρεται στο πόσο δύσκολο είναι να λυθεί, καθώς και στο πλήθος των επιλογών που πρέπει να εξεταστούν προκειμένου να φτάσει κανείς στη λύση. Στην περίπτωση ενός λαβύρινθου, η πολυπλοκότητα προκύπτει από το πλήθος των διασταυρώσεων, των διαδρόμων και των πιθανών αδιεξόδων. Παρόμοια, σε ένα υπολογιστικό πρόβλημα, η πολυπλοκότητα σχετίζεται με την επεξεργασία μεγάλων όγκων δεδομένων, πολλών συνθηκών και πιθανών λύσεων που πρέπει να εξεταστούν.
Οι αλγόριθμοι είναι ουσιαστικά σχεδιασμένοι να διαχειρίζονται αυτή την πολυπλοκότητα, καθώς επιτρέπουν τη συστηματική αναζήτηση της καλύτερης λύσης χωρίς να χρειάζεται να δοκιμάζονται όλες οι επιλογές τυχαία.
- Διερεύνηση και Εύρεση Βέλτιστης Διαδρομής
Όταν προσπαθούμε να λύσουμε ένα πρόβλημα που μοιάζει με λαβύρινθο, η βασική στρατηγική είναι η αναζήτηση. Ένας αλγόριθμος αναζήτησης διερευνά όλες τις πιθανές διαδρομές μέχρι να βρει τη σωστή. Αυτή η διαδικασία μπορεί να γίνει με διάφορους τρόπους, ανάλογα με τον αλγόριθμο που χρησιμοποιείται.
Οι πιο βασικές στρατηγικές που χρησιμοποιούνται σε τέτοιες καταστάσεις είναι:
– Εξάντληση των επιλογών: Στην πιο απλή περίπτωση, ένας αλγόριθμος μπορεί να δοκιμάσει κάθε πιθανή διαδρομή (δηλαδή εξαντλητική αναζήτηση), μέχρι να βρει τη σωστή. Αυτός ο τρόπος, όμως, μπορεί να είναι πολύ αργός για προβλήματα με πολλές επιλογές, καθώς χρειάζεται να ελεγχθούν όλες οι διαδρομές μία προς μία.
– Συστηματική προσέγγιση: Ένας αλγόριθμος μπορεί να εφαρμόσει μια πιο συστηματική μέθοδο, όπως την εξερεύνηση όλων των διαδρομών κοντά στο σημείο εκκίνησης πριν προχωρήσει σε πιο απομακρυσμένα μονοπάτια. Αυτό γίνεται με αλγορίθμους όπως η ευρεία αναζήτηση (BFS), που εγγυάται ότι θα βρεθεί η συντομότερη διαδρομή.
– Αλγοριθμική προσέγγιση με προγνωστικές ενδείξεις: Οι αλγόριθμοι που χρησιμοποιούν ευρετική προσέγγιση, όπως ο Α, επιταχύνουν τη διαδικασία αναζήτησης αξιολογώντας ποια διαδρομή είναι πιθανό να είναι η καλύτερη. Αυτή η προσέγγιση συνδυάζει την έρευνα και τη λήψη αποφάσεων, δίνοντας προτεραιότητα στα μονοπάτια που φαίνονται πιο αποδοτικά.
- Αλγόριθμοι και Βελτιστοποίηση
Η βελτιστοποίηση είναι ένας σημαντικός στόχος όταν εφαρμόζουμε αλγόριθμους σε προβλήματα πολυπλοκότητας, όπως οι λαβύρινθοι. Δεν αρκεί απλώς να βρούμε μια λύση· συχνά αναζητούμε τη **βέλτιστη** λύση, δηλαδή την καλύτερη ή πιο αποδοτική από πλευράς χρόνου και κόστους.
Για παράδειγμα, σε έναν λαβύρινθο, η απλή εύρεση της εξόδου μπορεί να είναι αρκετή, αλλά σε πολλά προβλήματα, η βέλτιστη λύση περιλαμβάνει τη γρηγορότερη ή την πιο οικονομική διαδρομή. Οι αλγόριθμοι βελτιστοποίησης μπορούν να χρησιμοποιηθούν για να εξασφαλίσουν ότι δεν θα χαθεί πολύτιμος χρόνος ή πόροι κατά τη διάρκεια της αναζήτησης.
Ένας από τους πιο γνωστούς αλγόριθμους βελτιστοποίησης είναι ο **αλγόριθμος Dijkstra**, που χρησιμοποιείται για την εύρεση της συντομότερης διαδρομής ανάμεσα σε δύο σημεία, ιδανικός για προβλήματα όπως η πλοήγηση σε δίκτυα. Αυτός ο αλγόριθμος εξετάζει συστηματικά τις πιθανές διαδρομές και επιλέγει εκείνη που έχει το μικρότερο κόστος.
- Πολυπλοκότητα Υπολογισμού
Οι αλγόριθμοι δεν αξιολογούνται μόνο με βάση την αποτελεσματικότητά τους στο να βρίσκουν λύσεις, αλλά και με βάση την υπολογιστική τους πολυπλοκότητα, δηλαδή το πόσο γρήγορα μπορούν να βρουν τη λύση ανάλογα με το μέγεθος του προβλήματος. Ένα μικρό πρόβλημα, όπως ένας μικρός λαβύρινθος, μπορεί να λυθεί γρήγορα με απλό τρόπο. Ωστόσο, καθώς αυξάνεται το μέγεθος του προβλήματος, αυξάνεται και η πολυπλοκότητα.
Η υπολογιστική πολυπλοκότητα μετριέται συχνά σε χρόνο (πόσα βήματα απαιτούνται για την επίλυση) και σε χώρο (πόση μνήμη χρησιμοποιείται). Οι αλγόριθμοι που έχουν σχεδιαστεί για την επίλυση μεγάλων και πολύπλοκων προβλημάτων πρέπει να είναι **αποδοτικοί**, έτσι ώστε να μην καταναλώνουν υπερβολικούς πόρους και να δίνουν λύση σε λογικό χρόνο.
- Αλγόριθμοι σε Πραγματικές Εφαρμογές
Οι αλγόριθμοι δεν είναι απλώς αφηρημένες μαθηματικές έννοιες. Εφαρμόζονται σε πραγματικά προβλήματα, από την πλοήγηση GPS μέχρι τη ρομποτική και τα δίκτυα υπολογιστών. Σε ένα σύστημα πλοήγησης, για παράδειγμα, η εύρεση της συντομότερης διαδρομής ανάμεσα σε δύο τοποθεσίες είναι ένα πρόβλημα λαβύρινθου. Οι αλγόριθμοι αναζήτησης χρησιμοποιούνται για να βρουν τη βέλτιστη διαδρομή, ενώ ταυτόχρονα λαμβάνονται υπόψη άλλοι παράγοντες, όπως η κίνηση ή τα εμπόδια.
Στη μηχανική μάθηση, οι αλγόριθμοι αναζητούν πρότυπα και βέλτιστες λύσεις μέσα από τεράστιες ποσότητες δεδομένων, και χρησιμοποιούν τεχνικές που βασίζονται στην ίδια ιδέα της αναζήτησης λύσεων σε πολυπλοκότητα. Ο τρόπος με τον οποίο “εκπαιδεύονται” τα μοντέλα μηχανικής μάθησης για να προβλέψουν ή να αναγνωρίσουν πρότυπα μοιάζει με τη λογική των αλγορίθμων αναζήτησης, καθώς εξετάζονται πολλές επιλογές και διαδρομές.
Συμπέρασμα
Η αναλογία του λαβύρινθου με τα προβλήματα πολυπλοκότητας είναι μια κλασική και αποτελεσματική μεταφορά για να κατανοήσουμε πώς λειτουργούν οι αλγόριθμοι. Μέσα από τον σχεδιασμό και την εφαρμογή αλγορίθμων, είμαστε σε θέση να επιλύουμε περίπλοκα προβλήματα με συστηματικό και αποδοτικό τρόπο. Από τις απλές αναζητήσεις μέχρι τις πιο προχωρημένες μεθόδους βελτιστοποίησης, οι αλγόριθμοι είναι απαραίτητα εργαλεία που μας βοηθούν να βρούμε τη σωστή διαδρομή, ανεξάρτητα από την πολυπλοκότητα του προβλήματος.
Είτε πρόκειται για την εξερεύνηση ενός λαβύρινθου είτε για την πλοήγηση μέσα σε ένα δίκτυο υπολογιστών ή δεδομένων, οι αλγόριθμοι μας προσφέρουν τον καλύτερο τρόπο για να διαχειριστούμε την πολυπλοκότητα και να φτάσουμε στη λύση με το βέλτιστο κόστος και χρόνο.

Η βελτιστοποίηση τοποθέτησης αποτελεί ένα κεντρικό ζήτημα σε πολλούς τομείς της επιστήμης και της τεχνολογίας. Από την οργάνωση αποθηκευτικών χώρων, τη διαχείριση μεταφορών και logistics, μέχρι τον προγραμματισμό και την υπολογιστική γεωμετρία, η αναζήτηση της βέλτιστης τοποθέτησης αντικειμένων σε περιορισμένους χώρους είναι κρίσιμη. Οι αλγόριθμοι είναι τα εργαλεία που μας επιτρέπουν να αντιμετωπίσουμε την πολυπλοκότητα αυτών των προβλημάτων με συστηματικό και αποδοτικό τρόπο, επιδιώκοντας την καλύτερη δυνατή λύση.
Τι είναι η βέλτιστη τοποθέτηση;
Η βέλτιστη τοποθέτηση αναφέρεται στην τοποθέτηση ενός συνόλου αντικειμένων μέσα σε έναν περιορισμένο χώρο με τέτοιο τρόπο ώστε να χρησιμοποιηθεί αυτός ο χώρος όσο το δυνατόν καλύτερα. Στόχος είναι να τοποθετηθούν όσο το δυνατόν περισσότερα αντικείμενα, χωρίς να αφήνονται κενά ή να σπαταλιέται πολύτιμος χώρος. Αυτό το πρόβλημα είναι κλασικό και εντοπίζεται σε εφαρμογές όπως:
– Αποθήκευση προϊόντων: Σε αποθήκες ή βιομηχανικά κέντρα, είναι σημαντικό τα εμπορεύματα να τοποθετούνται με τέτοιο τρόπο ώστε να μεγιστοποιείται η χωρητικότητα της αποθήκης.
– Φόρτωση εμπορευμάτων: Σε μεταφορικά μέσα, όπως φορτηγά, πλοία ή αεροπλάνα, η αποδοτική φόρτωση των προϊόντων μειώνει τον αριθμό των δρομολογίων και κατ’ επέκταση τα κόστη.
– Συσκευασία προϊόντων: Η οργάνωση προϊόντων μέσα σε συσκευασίες, κουτιά ή κοντέινερ πρέπει να βελτιστοποιηθεί, ώστε να χωρέσουν όσο το δυνατόν περισσότερα αντικείμενα.
Η πολυπλοκότητα των προβλημάτων τοποθέτησης
Η πολυπλοκότητα αυτών των προβλημάτων προκύπτει από τον μεγάλο αριθμό παραγόντων και παραμέτρων που πρέπει να ληφθούν υπόψη. Για παράδειγμα, τα αντικείμενα μπορεί να έχουν διαφορετικά μεγέθη και σχήματα, και ο διαθέσιμος χώρος μπορεί να έχει περιορισμούς. Κάθε αντικείμενο πρέπει να τοποθετηθεί με τέτοιο τρόπο ώστε να μην δημιουργούνται κενά και να αξιοποιείται πλήρως ο χώρος.
Σε τέτοια προβλήματα, δεν αρκεί απλά να βρούμε μια λύση· η πρόκληση είναι να βρεθεί η καλύτερη δυνατή λύση, δηλαδή αυτή που μεγιστοποιεί τη χωρητικότητα ή ελαχιστοποιεί το κόστος, ενώ παράλληλα μειώνει τα απόβλητα ή τις σπατάλες πόρων. Αυτή η αναζήτηση της βέλτιστης λύσης απαιτεί τη χρήση αλγορίθμων που μπορούν να χειριστούν πολλαπλές παραμέτρους ταυτόχρονα.
Αλγόριθμοι για τη βέλτιστη τοποθέτηση
Για την αντιμετώπιση της πολυπλοκότητας στη βελτιστοποίηση της χωροθέτησης, χρησιμοποιούνται διάφοροι αλγόριθμοι που αναπτύχθηκαν για να επιλύσουν τέτοιου είδους προβλήματα. Κάθε αλγόριθμος έχει τα δικά του πλεονεκτήματα και μειονεκτήματα, και χρησιμοποιείται ανάλογα με το συγκεκριμένο είδος του προβλήματος και τις απαιτήσεις του.
- Αλγόριθμοι Συσκευασίας (Packing Algorithms)
Οι αλγόριθμοι συσκευασίας προσπαθούν να τοποθετήσουν αντικείμενα μέσα σε έναν περιορισμένο χώρο, όπως ένα κουτί, μια αποθήκη ή ένα φορτηγό, με τρόπο που ελαχιστοποιεί τον κενό χώρο και αυξάνει την αποδοτικότητα. Ένα παράδειγμα τέτοιων προβλημάτων είναι το πρόβλημα συσκευασίας κουτιών (**box-packing problem**), στο οποίο πρέπει να τοποθετηθούν αντικείμενα διαφόρων μεγεθών σε κουτιά με συγκεκριμένες διαστάσεις.
Υπάρχουν διάφορες παραλλαγές αυτού του προβλήματος, ανάλογα με το αν τα αντικείμενα μπορούν να τοποθετηθούν κάθετα ή οριζόντια, αν επιτρέπονται επικαλύψεις, ή αν τα κουτιά έχουν σταθερό ή μεταβλητό μέγεθος.
- Αλγόριθμος Binning (Bin Packing Algorithm)
Ένας άλλος διαδεδομένος αλγόριθμος είναι ο αλγόριθμος bin packing, ο οποίος χρησιμοποιείται για την τοποθέτηση αντικειμένων σε “δοχεία” (bins). Στόχος είναι να τοποθετηθούν τα αντικείμενα με τέτοιο τρόπο ώστε να χρησιμοποιηθούν όσο το δυνατόν λιγότερα δοχεία, αποφεύγοντας τον άχρηστο χώρο. Αυτός ο αλγόριθμος βρίσκει εφαρμογή στη διαχείριση αποθεμάτων, στις μεταφορές και στη διανομή προϊόντων.
- Ευρετικοί αλγόριθμοι
Σε περιπτώσεις όπου τα προβλήματα χωροθέτησης γίνονται εξαιρετικά πολύπλοκα (λόγω του πλήθους των αντικειμένων, των παραμέτρων ή των περιορισμών), οι ευρετικοί αλγόριθμοι χρησιμοποιούνται για να βρουν αποδεκτές λύσεις μέσα σε λογικό χρονικό διάστημα. Οι ευρετικές μέθοδοι δεν εγγυώνται τη βέλτιστη λύση, αλλά παρέχουν μια λύση που είναι κοντά στη βέλτιστη, χωρίς να απαιτούν υπερβολικούς υπολογιστικούς πόρους. Οι αλγόριθμοι γενετικής (genetic algorithms) και οι αλγόριθμοι προσομοιωμένης ανόπτησης (simulated annealing) είναι παραδείγματα ευρετικών μεθόδων που χρησιμοποιούνται σε προβλήματα βελτιστοποίησης.
- Αλγόριθμοι Γραμμικού Προγραμματισμού
Για πιο ακριβείς λύσεις, χρησιμοποιούνται συχνά αλγόριθμοι γραμμικού προγραμματισμού. Αυτοί οι αλγόριθμοι επιτρέπουν την επίλυση προβλημάτων βελτιστοποίησης με τη βοήθεια μαθηματικών μοντέλων που χρησιμοποιούν εξισώσεις και ανισώσεις για να καθορίσουν τις καλύτερες δυνατές λύσεις.
Οι αλγόριθμοι γραμμικού προγραμματισμού είναι πολύ αποδοτικοί σε προβλήματα με αυστηρούς περιορισμούς και χρησιμοποιούνται σε εφαρμογές όπως η κατανομή πόρων, η διαχείριση παραγωγής, και οι μεταφορές.
Προκλήσεις και Υπολογιστική Πολυπλοκότητα
Το βασικό πρόβλημα στη βελτιστοποίηση της χωροθέτησης είναι ότι τα προβλήματα αυτά έχουν μεγάλη υπολογιστική πολυπλοκότητα. Καθώς αυξάνεται το πλήθος των αντικειμένων ή των παραμέτρων που πρέπει να εξεταστούν, αυξάνεται και η πολυπλοκότητα του προβλήματος. Η αναζήτηση της βέλτιστης λύσης γίνεται εκθετικά πιο δύσκολη, καθώς κάθε προσθήκη αντικειμένων ή περιορισμών πολλαπλασιάζει τον αριθμό των πιθανών διατάξεων.
Γι’ αυτόν τον λόγο, οι ακριβείς αλγόριθμοι μπορεί να είναι αναποτελεσματικοί σε προβλήματα μεγάλης κλίμακας, και προτιμώνται ευρετικές μέθοδοι που δίνουν γρήγορες και αποδεκτές λύσεις.
Εφαρμογές στην πραγματική ζωή
Τα προβλήματα βελτιστοποίησης της τοποθέτησης και της χωροθέτησης εμφανίζονται σε πολλές εφαρμογές της πραγματικής ζωής:
– Στη βιομηχανία: Οι αλγόριθμοι χωροθέτησης χρησιμοποιούνται για τη βελτιστοποίηση της διάταξης προϊόντων στις αποθήκες, την κατανομή εμπορευμάτων στα μέσα μεταφοράς και την οργάνωση των συστημάτων αποθήκευσης.
– Στις μεταφορές: Οι αλγόριθμοι βελτιστοποίησης εξασφαλίζουν ότι τα οχήματα μεταφοράς χρησιμοποιούνται με τον αποδοτικότερο τρόπο, μειώνοντας τα κόστη και βελτιώνοντας την απόδοση.
– Στην καθημερινή ζωή: Η βελτιστοποίηση της συσκευασίας, όπως η τοποθέτηση αντικειμένων σε μια βαλίτσα, είναι ένα μικρής κλίμακας πρόβλημα χωροθέτησης που όλοι
Συμπέρασμα
Η βελτιστοποίηση της τοποθέτησης είναι ένα πρόβλημα που εμφανίζεται σε πολλές πτυχές της καθημερινής ζωής και της βιομηχανίας. Οι αλγόριθμοι που αναζητούν την καλύτερη δυνατή λύση σε τέτοια προβλήματα αποτελούν κρίσιμο εργαλείο για τη μείωση της σπατάλης χώρου και πόρων, τη βελτίωση της απόδοσης και την εξοικονόμηση κόστους. Καθώς τα προβλήματα αυτά γίνονται πιο πολύπλοκα, οι αλγόριθμοι και οι μέθοδοι βελτιστοποίησης συνεχίζουν να εξελίσσονται, προσφέροντας λύσεις που βοηθούν να επιτευχθεί η μέγιστη αποδοτικότητα σε έναν κόσμο με περιορισμένους πόρους και αυξημένες απαιτήσεις.
«Ψηφιακοί καλλιτέχνες» (20 λεπτά)

Ψηφιακό και αναλογικό – Ψηφιοποίηση και ψηφιακές εικόνες
Η ψηφιοποίηση είναι η διαδικασία μετατροπής της αναλογικής πληροφορίας σε ψηφιακή μορφή, καθιστώντας την κατανοητή και διαχειρίσιμη από υπολογιστικά συστήματα. Με τη μετάβαση από το αναλογικό στο ψηφιακό, η πληροφορία γίνεται πιο ευέλικτη και αποδοτική στη χρήση της, επιτρέποντας την αποθήκευση, την επεξεργασία και τη μετάδοσή της με υψηλή ακρίβεια και μικρότερο κόστος. Αυτό το πέρασμα στην ψηφιακή εποχή είχε τεράστιο αντίκτυπο σε πολλές πτυχές της καθημερινής ζωής, όπως στις επικοινωνίες, την ψυχαγωγία, τις τέχνες, την επιστήμη και τη βιομηχανία.
Αναλογικό και Ψηφιακό: Βασικές Διαφορές
Για να κατανοήσουμε πλήρως την ψηφιοποίηση, πρέπει πρώτα να καταλάβουμε τη διαφορά μεταξύ αναλογικής και ψηφιακής πληροφορίας.
– Αναλογική πληροφορία: Η αναλογική πληροφορία είναι συνεχής και κυμαίνεται με σταθερό τρόπο, αντιπροσωπεύοντας αδιάκοπες μεταβολές στη φυσική κατάσταση της πληροφορίας. Για παράδειγμα, ο ήχος που ακούμε είναι αναλογικός επειδή αποτελείται από κυματομορφές που συνεχώς αλλάζουν την έντασή τους και τη συχνότητά τους. Η αναλογική πληροφορία εκφράζεται σε απεριόριστες τιμές και δεν έχει διακριτές μονάδες. Τα αναλογικά σήματα, όπως αυτά των βινυλίων, των κασετών και των ραδιοφωνικών κυμάτων, αλλάζουν με ροή και συχνά επηρεάζονται από τον θόρυβο και τις αλλοιώσεις λόγω περιβαλλοντικών παραγόντων ή φθοράς.
– Ψηφιακή πληροφορία: Σε αντίθεση, η ψηφιακή πληροφορία είναι διακριτή, δηλαδή αναλύεται σε διακριτές μονάδες, συνήθως με τη μορφή δυαδικών δεδομένων (bits), όπου κάθε τιμή μπορεί να είναι είτε 0 είτε 1. Η ψηφιακή πληροφορία δεν κυμαίνεται συνεχώς, αλλά μετατρέπεται σε έναν ακολουθιακό αριθμό δεδομένων που μπορούν να επεξεργαστούν και να αναπαραχθούν με ακρίβεια από υπολογιστές. Ένα χαρακτηριστικό παράδειγμα είναι οι εικόνες που αποτελούνται από pixels, τα οποία αποθηκεύουν χρώματα και εντάσεις φωτός ως αριθμητικές τιμές.
Η διαδικασία της ψηφιοποίησης
Η ψηφιοποίηση είναι η διαδικασία μετατροπής αναλογικών δεδομένων σε ψηφιακά. Πρόκειται για μια διαδικασία που βασίζεται σε δύο βήματα:
- Δειγματοληψία (Sampling): Σε αυτό το στάδιο, το αναλογικό σήμα λαμβάνεται σε διακριτά χρονικά διαστήματα. Αντί να καταγραφεί η συνεχής ροή της πληροφορίας, καταγράφονται συγκεκριμένα σημεία κατά μήκος του σήματος. Όσο περισσότερα δείγματα ληφθούν, τόσο πιο πιστή θα είναι η αναπαράσταση του αρχικού αναλογικού σήματος.
- Κβαντοποίηση (Quantization): Αφού ληφθούν τα δείγματα, η τιμή της πληροφορίας κάθε δείγματος μετατρέπεται σε μια αριθμητική τιμή, που αντιπροσωπεύει την πλησιέστερη δυνατή ψηφιακή αντιστοιχία. Οι τιμές αυτές κωδικοποιούνται ως bits. Όσο μεγαλύτερη είναι η ανάλυση της κβαντοποίησης (δηλαδή, όσο περισσότερα bits χρησιμοποιούνται για την κωδικοποίηση), τόσο πιο ακριβής είναι η ψηφιακή αναπαράσταση.
Ψηφιακές Εικόνες και Pixels
Ένα από τα πιο εμφανή παραδείγματα ψηφιοποίησης είναι οι ψηφιακές εικόνες. Όταν μια εικόνα ψηφιοποιείται, διασπάται σε ένα δίκτυο μικροσκοπικών μονάδων που ονομάζονται pixels. Κάθε pixel περιέχει πληροφορίες για το χρώμα και τη φωτεινότητα σε μια συγκεκριμένη θέση στην εικόνα. Έτσι, η αρχική αναλογική εικόνα μετατρέπεται σε ένα σύνολο δεδομένων, τα οποία αποθηκεύονται ψηφιακά και μπορούν να αναπαραχθούν, να επεξεργαστούν ή να μεταδοθούν.
Η ανάλυση μιας ψηφιακής εικόνας εξαρτάται από το πλήθος των pixels. Όσο περισσότερα pixels έχει μια εικόνα, τόσο πιο υψηλής ανάλυσης είναι, κάτι που επιτρέπει την αναπαραγωγή λεπτομερειών. Παράδειγμα είναι μια φωτογραφία υψηλής ανάλυσης, όπου εκατομμύρια pixels συνδυάζονται για να αναπαραστήσουν με ακρίβεια την αρχική εικόνα. Πλεονεκτήματα της Ψηφιοποίησης
Η ψηφιοποίηση προσφέρει πολυάριθμα πλεονεκτήματα σε σύγκριση με τις αναλογικές μορφές πληροφορίας:
- Αποθήκευση και ανάκτηση: Τα ψηφιακά δεδομένα μπορούν να αποθηκευτούν με ασφάλεια και να αναπαραχθούν χωρίς απώλειες ποιότητας. Σε αντίθεση με τις αναλογικές μορφές, που μπορεί να φθαρούν με τον καιρό, τα ψηφιακά δεδομένα μπορούν να παραμείνουν αμετάβλητα ανεξάρτητα από το πόσες φορές αναπαράγονται ή αντιγράφονται.
- Ακρίβεια και ευκρίνεια: Τα ψηφιακά δεδομένα είναι πολύ πιο ακριβή και μπορούν να αναπαραχθούν χωρίς να επηρεάζονται από θορύβους ή παραμορφώσεις. Για παράδειγμα, μια ψηφιακή εικόνα μπορεί να διατηρήσει την ίδια ποιότητα ανεξάρτητα από το πόσες φορές αποθηκεύεται ή επεξεργάζεται.
- Επεξεργασία: Η ψηφιακή πληροφορία είναι πολύ πιο εύκολο να επεξεργαστεί. Εικόνες, ήχοι, βίντεο και κείμενα μπορούν να τροποποιηθούν, να βελτιωθούν ή να αναπαραχθούν μέσω λογισμικών επεξεργασίας, επιτρέποντας τη δημιουργία καινοτόμων έργων και την αποκατάσταση παλαιότερων αρχείων.
- Μετάδοση και διανομή: Τα ψηφιακά δεδομένα μπορούν εύκολα να διαμοιραστούν και να μεταδοθούν μέσω του διαδικτύου ή άλλων ψηφιακών δικτύων, επιτρέποντας την ταχύτατη διάδοση πληροφοριών. Για παράδειγμα, ψηφιακά βίντεο μπορούν να μεταδοθούν σε όλο τον κόσμο μέσα σε δευτερόλεπτα, μέσω υπηρεσιών streaming.
- Ασφάλεια και προστασία: Η ψηφιακή μορφή επιτρέπει τη χρήση τεχνολογιών κρυπτογράφησης και ασφάλειας για την προστασία των δεδομένων από μη εξουσιοδοτημένη πρόσβαση ή τροποποίηση. Τα ψηφιακά αρχεία μπορούν επίσης να δημιουργήσουν πολλαπλά αντίγραφα ασφαλείας, ώστε να διασφαλιστεί η ακεραιότητα των δεδομένων.
Εφαρμογές της Ψηφιοποίησης
Η ψηφιοποίηση έχει επηρεάσει ποικίλους τομείς της καθημερινής ζωής:
– Ψηφιακή φωτογραφία και τέχνη: Η ψηφιοποίηση των εικόνων επιτρέπει τη διατήρηση και τη δημιουργία ψηφιακών έργων τέχνης, καθώς και τη γρήγορη επεξεργασία και κοινή χρήση φωτογραφιών.
– Ψηφιακή μουσική και ήχος: Οι ήχοι, όπως η μουσική και οι ηχογραφήσεις, μετατρέπονται σε ψηφιακά αρχεία (π.χ. MP3, WAV), διευκολύνοντας την αποθήκευση, την αναπαραγωγή και τη μετάδοσή τους.
– Βίντεο και κινηματογράφος: Οι ταινίες και τα βίντεο που βλέπουμε πλέον έχουν ψηφιοποιηθεί, επιτρέποντας την ταχεία επεξεργασία και τη διάδοσή τους μέσω ψηφιακών πλατφορμών, όπως το YouTube ή τα συστήματα streaming.
– Σαρωτές και αρχεία: Με τη χρήση σαρωτών, τα έγγραφα, τα βιβλία και οι εικόνες μπορούν να ψηφιοποιηθούν, επιτρέποντας την αποθήκευση και τη διάθεσή τους σε ψηφιακές βιβλιοθήκες.
Συμπέρασμα
Η ψηφιοποίηση αποτελεί έναν ακρογωνιαίο λίθο της σύγχρονης τεχνολογίας. Μετατρέποντας την αναλογική πληροφορία σε ψηφιακή, η πληροφορία γίνεται πιο εύκολα διαχειρίσιμη, αποθηκεύσιμη και αναπαραγώγιμη. Αυτή η διαδικασία έχει αλλάξει τον τρόπο που εργαζόμαστε, επικοινωνούμε, δημιουργούμε και αποθηκεύουμε δεδομένα, προσφέροντας αμέτρητες δυνατότητες και βελτιώσεις στην καθημερινή μας ζωή και σε όλους τους κλάδους της τεχνολογίας.
«Στη φαντασία ενός ρομπότ» (20 λεπτά)
Αρχές λειτουργίας φρυκτωριών
Οι Αρχαίοι Έλληνες χρησιμοποιούσαν ένα καλά οργανωμένο επικοινωνιακό δίκτυο ανά τον Ελλαδικό χώρο. Το δίκτυο αυτό, το λεγόμενο δίκτυο των Φρυκτωριών, εκμεταλλευόμενο τα νησιά του Αιγαίου και την ορεινή μορφολογία της περιοχής, χρησιμοποιούσε την φωτιά και έναν κώδικα αναπαράστασης γραμμάτων για την μετάδοση μηνυμάτων σε πολλά χιλιόμετρα.
Τα σημεία τα οποία χρησιμοποιούσαν οι αρχαίοι Έλληνες ήταν κατά κανόνα σε πλεονεκτικές θέσεις, κορυφές βουνών ή ακρωτήρια νησιών, τα οποία πρόσφεραν μεγάλη (μακρινή) οπτική επαφή. Σε πολλές κορυφές υπάρχουν ακόμα και σήμερα ερείπια ή κτίσματα, τα οποία ήταν φρυκτωρίες στην αρχαιότητα. Αξίζει να σημειωθεί πως οι θέσεις και οι προσανατολισμοί των δικτύων των φρυκτωριών τουλάχιστον στον ελλαδικό χώρο συμπίπτουν και με τις θέσεις που βρίσκονται οι σημερινοί τηλεπικοινωνιακοί αναμεταδότες.
Οι φρυκτωρίες αποτελούν μία συστηματική μέθοδος μετάδοσης προσυμφωνημένων μηνυμάτων με χρήση φωτιάς. Οι πρώτες φρυκτωρίες (ή φρυκτώρια) θεωρούνται κατά πολλούς οι Ηράκλειες στήλες στο Γιβραλτάρ. Τις φρυκτωρίες χρησιμοποίησε αρχικά ο μυκηναϊκός πολιτισμός.
Οι θεμελιώδεις αρχές λειτουργίας των φρυκτωριών είναι ίδιες με αυτές που χρησιμοποιούνται σήμερα. Δηλαδή, για την αποκωδικοποίηση των πληροφοριών ακολουθείται ένα συγκεκριμένο πρωτόκολλο βάσει του οποίου μεταφέρονται τα τελικά δεδομένα από τον ένα σταθμό στον άλλο.
Κρυπτογράφηση – Αποκρυπτογράφηση
Η κρυπτολογία είναι η επιστήμη η οποία αποτελείται από τους εξής δύο κλάδους: την κρυπτογραφία και την κρυπτανάλυση. Στόχος της είναι η μελέτη της ασφαλούς επικοινωνίας εφαρμόζοντας τα μαθηματικά καθώς την θεωρητική πληροφορική.
Πιο συγκεκριμένα, κύριος στόχος της είναι να παρέχει μηχανισμούς ώστε δύο ή περισσότερα άκρα επικοινωνίας, όπως για παράδειγμα οι άνθρωποι, τα προγράμματα υπολογιστών και άλλα, να ανταλλάζουν μηνύματα, χωρίς ωστόσο κάποιος τρίτος να είναι σε θέση να έρθει σε επαφή με την περιεχόμενη πληροφορία (εκτός από τα δύο κύρια άκρα).
Ιστορικά, η κρυπτογραφία χρησιμοποιήθηκε για τη μετατροπή της πληροφορίας μηνυμάτων από μια κανονική, κατανοητή μορφή σε έναν άλυτο «γρίφο», που χωρίς τη γνώση του κρυφού μετασχηματισμού θα παρέμενε ακατανόητος. Κύριο χαρακτηριστικό των παλαιότερων μορφών κρυπτογράφησης ήταν ότι η επεξεργασία γινόταν πάνω στη γλωσσική δομή του μηνύματος.
Στις νεότερες μορφές της, όμως, η κρυπτογραφία χρησιμοποιεί το αριθμητικό ισοδύναμο, ενώ η έμφαση έχει μεταφερθεί σε διάφορα πεδία των μαθηματικών, όπως διακριτά μαθηματικά, θεωρία αριθμών, θεωρία πληροφορίας, υπολογιστική πολυπλοκότητα, στατιστική και συνδυαστική ανάλυση.
Η κρυπτογράφηση και αποκρυπτογράφηση ενός μηνύματος γίνεται με τη βοήθεια ενός αλγόριθμου κρυπτογράφησης (cipher) και ενός κλειδιού κρυπτογράφησης (key). Συνήθως ο αλγόριθμος κρυπτογράφησης είναι γνωστός, οπότε η εμπιστευτικότητα του κρυπτογραφημένου μηνύματος που μεταδίδεται βασίζεται στη μυστικότητα του κλειδιού κρυπτογράφησης. Το μέγεθος του κλειδιού κρυπτογράφησης μετριέται σε αριθμό bits. Όσο μεγαλύτερο είναι το κλειδί κρυπτογράφησης, τόσο δυσκολότερα μπορεί να αποκρυπτογραφηθεί το κρυπτογραφημένο μήνυμα από επίδοξους εισβολείς, δηλαδή τόσο πιο ασφαλές είναι. Διαφορετικοί αλγόριθμοι κρυπτογράφησης απαιτούν διαφορετικά μήκη κλειδιών για να πετύχουν το ίδιο επίπεδο ανθεκτικότητας κρυπτογράφησης.

Με τον όρο «τεχνητή νοημοσύνη» αναφερόμαστε στον κλάδο της πληροφορικής ο οποίος ασχολείται με τη σχεδίαση και την υλοποίηση υπολογιστικών συστημάτων που μιμούνται στοιχεία της ανθρώπινης συμπεριφοράς τα οποία υπονοούν έστω και στοιχειώδη ευφυΐα, όπως μάθηση, προσαρμοστικότητα, εξαγωγή συμπερασμάτων, κατανόηση από τα συμφραζόμενα, επίλυση προβλημάτων και άλλα.
Η τεχνητή νοημοσύνη αποτελεί σημείο τομής μεταξύ πολλαπλών επιστημών όπως της πληροφορικής, της ψυχολογίας, της φιλοσοφίας, της επιστήμης μηχανικών και άλλων επιστημών με στόχο τη σύνθεση ευφυούς συμπεριφοράς, με στοιχεία συλλογιστικής, μάθησης και προσαρμογής στο περιβάλλον. Η τεχνητή νοημοσύνη εφαρμόζεται τόσο σε μηχανές, όσο και σε υπολογιστές ειδικής κατασκευής και χωρίζεται σε 2 κατηγορίες:
1) Συμβολική τεχνητή νοημοσύνη: η οποία επιχειρεί να εξομοιώσει την ανθρώπινη νοημοσύνη αλγοριθμικά χρησιμοποιώντας σύμβολα και λογικούς κανόνες υψηλού επιπέδου
2) στην υποσυμβολική τεχνητή νοημοσύνη: η οποία αναπαράγει την ανθρώπινη ευφυΐα χρησιμοποιώντας στοιχειώδη αριθμητικά μοντέλα που συνθέτουν επαγωγικά νοήμονες συμπεριφορές κάνοντας χρήση διαδοχικών απλούστερων δομικών συστατικών.
Ανάλογα με τον εκάστοτε επιστημονικό στόχο της, η τεχνητή νοημοσύνη κατηγοριοποιείται και σε άλλου τύπου τομείς όπως επίλυση προβλημάτων, μηχανική μάθηση, ανακάλυψη γνώσης, συστήματα γνώσης και άλλα. Επίσης μπορεί να συνδυαστεί και με άλλους τομείς όπως μηχανική όραση και ρομποτική, τομείς που αποτελούν ανεξάρτητα πεδία εφαρμογής της. Η πιο εντυπωσιακή και γνωστή σε όλο τον κόσμο εφαρμογή της τεχνητής νοημοσύνης είναι το ανθρωποειδές «ρομπότ Σοφία». Κατασκευάστηκε το 2016 από τον καθηγητή Ντέιβιντ Χάνσον (ιδιοκτήτη της εταιρείας Hanson Robotics) και είναι το πρώτο ρομπότ που κατάφερε να μιμηθεί την ανθρώπινη συμπεριφορά, να δείξει τα συναισθήματά του και να συζητήσει με τους ανθρώπους. Μπορεί να μιλήσει πάνω από 20 γλώσσες ανάμεσα σε αυτές και τα Ελληνικά.